Реферат: Синтез и анализ аналоговых и цифровых регуляторов

Так как в системе имеет мести фиксатор нулевого порядка с передаточной функцией вида:

, (4.1)

то с учетом того, что z = e ^–pT , эту функцию можно записать в следующем далее виде:

. (4.2)

Сомножитель 1/р относят к линейной части, поэтому передаточная функция приведенной непрерывной части может быть записана в следующем виде:

. (4.3)

Так как

,

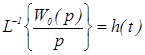переходная фнукция ленейной части системы, то z – передаточную функцию линейной части находим по следующему выражению:

. (4.4)

Найдем выражение для передаточной функции линейной части:

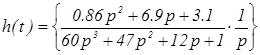. (4.5)

Для вычисления h(t) воспользуемся методом неопределенных коэффициентов. Необходимо определить полюса. Для этого необходимо найти корни следйющего уравнения:

()*р = 0.

Решив данное уравнение мы получили , что его корни следующего вида:

p₁ = 0;

p₂ = - 0,2;

p₃ = - 0,33;

p₄ = -0,25.

Переходная функция линейной части имеет следующий вид:

h(t) = -21,93e^-0.2t –4.03e^-0.33t +22.86e^-0.25t +3.1 . (4.6)

С учетом формулы (4.4) получаем

.

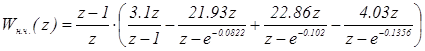После раскрытия скобок и приведения подобных мы получаем равенство в следующем виде:

. (4.7)

Результирующая передаточная функция разомкнутой системы может быть определена как произведение передаточной функции приведенной непрерывной чати и передаточной функции цифрового фильтра:

. (4.8)

Дискретная передаточная функция замкнутой системы:

. (4.9)

Определим значение W₃ (z) для каждой из систем:

- система с П – регулятором. W_р (z) = 1.01, W_н.ч. (z) – определеня по формуле (4.7), тогда:

; (4.10)

- система с ПИ – регулятором.

;

W_н.ч. (z) – определена по формуле (4.7), тогда:

; (4.11)

- система с ПИД – регулятором.

,

W_н.ч. (z) – определена по формуле (4.7), тогда:

. (4.12)

После того , как получим выражение дискрктных передаточных функций для всех систем, проанализируем устойчивость этих систем по критерию Джури.

Критерий устойчивости заключается в следующем.

Пусть задан А(z) – характкристический полином:

A(z) = a₀ zⁿ + a₁ ^n-1 + … + a_n , a₀ > 0.

Введем понятие обратного полинома, получаемого перестановкой коэффициентов исходного в обратном порядке:

A(z) = a_n zⁿ + a_n-1 ^n-1 + … + a₀ .

Разделим A(z) на обратной ему. В итоге получаем частное от деления число q₀ и остаток А₁ (z) – полином n-1 степени.

Домножим полученый результат на z^-1 получаем:

A₁ (z) = (a₀ -a_n q₀ )z^n-1 + … + (a_n-1 -a₁ q₀ ).

Затем делим остаток A₁ (z) на обратный ему A₁₀ (z) и определяем новое q₁ и A₂ (z)

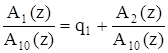и т.д.

Выполняя деление полиномов A_i (z) на обратные ему A_i0 (z), получаем последовательность чисел q_i = {q₀ , q₁ , q₂ ,…,q_n-2 }.

Необходимым и достаточным условием устойчивости цифровой системы является неравенства:

А(1)=(a₀ + a₁ + a₂ +…+a_n )>0;

(-1)ⁿ А(-1)=(a₀ (-1)ⁿ + a₁ (-1)^n-1 +…+a_n )>0;

|q_i |<1, i=0,1,2,…,n-2.

Используя выше изложенное, определим устойчивость наших систем.