Реферат: Синтез и анализ аналоговых и цифровых регуляторов
Для вычисления f[n] найдем полюса функции
.
Полюся функции:
z1 = 1;
z2 = -0,021;
z3 = 0,84;
z4 = 0,935-j0,171;
z5 = 0,935+j0,171;
z6 =0,98.
Производная знаменателя функции:
B’ (z) = 6z5 -23.347 z4 +34.893 z3 -24.39 z2 +7.505z-0.660
Подставим значение полюсов функции и значение производной в формулу (4.13), получим выражение для f[n]:
где а = z1 ;
b = z2 ;
c = z3 ;
d = z4 ;
e = z5 ;
f = z6 .
Изобразим переходый процесс на рисунке 4.4
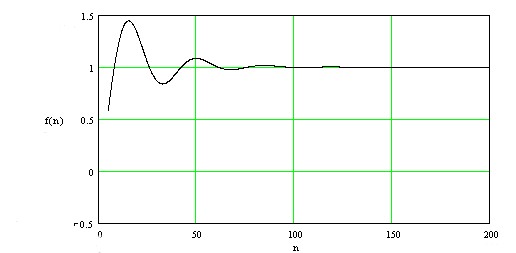
Рисунок 4.4 - Переходный процесс в системе с ПИД – регулятором.
5 Расчет цифрового фильтра
Для расчета цифрового фильтра, переводящего линейную часть из начального в конечное состояние за минимальное число периодов квантования и обеспечивающего ограничение на заданное управляющие воздействие, необходимо вычислить минимально возможный период квантования, но чтобы было удовлетворено условие:
|Um – q0 |£0,05, (5.1)
где Um = 1,0.
Вычисление значения q0 следует начать с определения значений коэффициентов числителя Z-передаточной функции приведенной непрерывной части для принятого периода дискретности. Пусть Z-передаточная функция приведенной непрерывной части представима в виде:
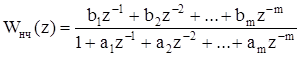. (5.2)
Тогда Z-передаточная функция оптимального по быстродействию цифрового фильтра Wф (z) имеет вид:
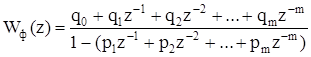, (5.3)
где pi = bi q0 , i = 1,2,…,m;
qi = ai q0 , i = 1,2,…,m;
.
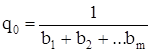Воспользуясь формулой (4.7) для Wнч (z) . Находим функции bi , аi и Т0 .
Для коэффициентов bi имеем:
; (5.4)
;(5.5)
. (5.6)
Для коэффициентов аi имеем:
; (5.7)
; (5.8)
. (5.9)
Найдем выражение для q0 :
. (5.10)
Определим Т0 при котором выполняется условие (5.1), для этого построим график зависимости и изибразим его на следующем рисунке 5.1.
