Реферат: Синтез и анализ аналоговых и цифровых регуляторов

A₄ (z)=-0,0305301+1.028762z.

В результате расчетов получили, чтоq₀ , q₁ , q₂ по модулю меньше еденицы, таким образом все три неравенства выполняются. Следовательно цифровая система устойчива.

После того, как определили устойчивость системы по критерию Джури, необходимо построить переходный процессы в замкнутых цифровых системах.

Для построения переходных процессов в замкнутых цифровых системах воспользуемся обратным z-преобразованием.

Eсли функция имеет m-полюсов z_k ={z₁ , z₂ ,…, z_n } , то:

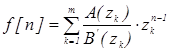, (4.13)

где A(z_k ) – числитель функции W₃ (z);

B^’ (z_k ) – производная знаменателя функции W₃ (z);

Замкнутая система с П – регулятором.

Передаточная функция для цифровой замкнутой системы с П-регулятором имеет вид:

Переходная функция замкнутой системы равна:

.

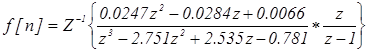Для вычисления f[n] найдем полюса функции

.

Полюся функции:

z₁ = 1;

z₂ = 0,8422;

z₃ = 0,954 – j0,313;

z₄ = 0,954 – j0,313.

Производная знаменателя функции:

B^’ (z) = -11.25z² +10.574z-3.317+4z³ .

Подставим значение полюсов функции и значение производной в формулу (4.13), получим выражение для :

где a = z₁ ;

b = z₂ ;

c = z₃ ;

d = z₄ ;

Изобразим переходый процесс на рисунке 4.2

Рисунок 4.2 - Переходный процесс в системе с П – регулятором

Замкнутая система с ПИ – регулятором.

Передаточная функция для цифровой замкнутой системы с ПИ-регулятором имеет вид:

;.

Переходная функция замкнутой системы равна:

.

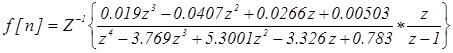Для вычисления f[n] найдем полюса функции

.

Полюся функции:

z₁ = 1;

z₂ = 0.847;

z₃ = 0.965;

z₄ = 0.973 – j0.0113;

z₅ = 0.973 + j0.0113.

Производная знаменателя функции:

B^’ (z) = 5z⁴ -19.027z³ +27.171 z² -17.253z+4.110

Подставим значение полюсов функции и значение производной в формулу (4.13), получим выражение для f[n]:

где а = z₁ ;

b = z₂ ;

c = z₃ ;

d = z₄ ;

e = z₅ ;

Изобразим переходый процесс на рисунке 4.3

Рисунок 4.3 - Переходный процесс в системе с ПИ – регулятором

Замкнутая система с ПИД – регулятором.