Реферат: Теория поля и элементы векторного анализа

4) Поток вектора через поверхность. Дивергенция

– поток векторной величины через элементарную площадку (элементарный поток)

(11)

векторный поток через незамкнутую площадку;

(12)

поток вектора через замкнутую площадку.

–

поток вектора скорости через поверхность S равен объему жидкости, протекающей через эту площадку поверхности за единицу времени.

По теореме Остроградского-Гаусса (рис. 7)

(13)

Сжимая объем и, следовательно получим, используя теорему осреднения

(14)

Следовательно, можно определить как предел

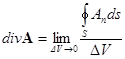(15)

Пример :

В гидродинамике поле скоростей имеет

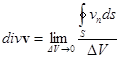
дивергенция равна количеству жидкости, рассчитанному на единицу объема, вытекающему из данной точки пространства за одну секунду, т.е. равна мощности источника жидкости (если > 0).

Если < 0, то в этих точках пространства расположен сток жидкости, с мощностью .

5. Циркуляция вектора вдоль линии

Роток векторного поля

Элементарная циркуляция вектора вдоль линии dl равна (рис. 8а)

(16)

Циркуляция вектора вдоль замкнутой линии L (рис. 8б)

(17)

Пусть контур L ограничивает некоторую поверхность S (рис. 8в). Используем теорему Стокса и преобразуем интеграл по кривой L в интеграл по поверхности S :

(18)

Роток (вихрь) вектора определяется как