Определение

Циркуляция вектора вдоль замкнутого контура равна потоку его ротора через поверхность, ограниченную этим контуром (рис. 9)

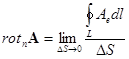(20)

Потенциальное векторное поле

Определение :

Векторное поле называется потенциальным, если существует скалярная величина , такая, что

– называется скалярным потенциалом поля.

Свойства потенциального поля

1. В потенциальном поле отсутствуют вихри (отсутствует ротация), т.е.

Доказательство:

2. Циркуляция по любому замкнутому контуру равна нулю (это следствие п.1)

3. Работа потенциального поля при перемещении точки из одного положения в другое не зависит от пути соединяющего эти положения и равна разности потенциалов в конечных точках.

Циркуляция потенциального поля не зависит от вида кривой, соединяющей две различные точки, и равна разности значений потенциала в данных точках.

отсюда получаем

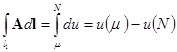
4. Векторные линии потенциального поля не могут быть замкнутыми.

Доказательство от противоположного:

Допустим, что есть замкнутая векторная линия L . Тогда по определению векторной линии вдоль соответствующего контура и, следовательно, и циркуляция по нему больше нуля , что противоречит свойству 2.

5. Сумма потенциальных векторных полей является потенциальным полем, и потенциал суммы полей равен сумме потенциалов.

Соленоидальное векторное поле

Определение :

Векторное поленазывается соленоидальным (вихревым), если существует векторная величина такая, что

= rot