Реферат: Теория устойчивости систем

Для устойчивости системы должно выполняться условие:

cn>0, cn-1>0, a13>0, a14>0, …, a1,n+1>0.

Пример: задано характеристическое уравнение

D(p)=0.104p7+0.33p6+5.5p5+15.5p4+25p3+25p2+19.7p+9.5=0

Определим устойчивость системы. Для этого построим таблицу Рауса:

Коэффициенты	an=0.104	an-2=5.5	an-4=25	an-6=19.7
ri	an-1=0.33	an-3=15.5	an-5=25	an-7=9.5
r0=0.315	0.6	17.1	1.7	0
r1=0.55	6.0	15.8	9.5	0
r2=0.1	15.52	15.75	0	0
r3=0.386	9.7	9.5	0	0
r4=1.6	0.55	0	0	0
r5=0	9.5	0	0	0

Все коэффициенты первой графы положительны, следовательно, система устойчива

7. Второй метод Ляпунова

Второй, или прямой, метод Ляпунова позволяет исследовать устойчивость решений нелинейных дифференциальных уравнений, не производя решения самих уравнений. Мы будем исследовать устойчивость тривиального решения автономных систем дифференциальных уравнений, то есть систем уравнений вида

(1)

При этом мы предполагаем, что функции fi(x1,…,xn) имеют непрерывные частные производные по всем аргументам в некоторой выпуклой области G : <Hn-мерного пространства. В этом случае в области G система уравнений (1) удовлетворяет условиям теоремы существования и единственности решения.

Рассмотрим функции V( x1,…,xn), определенные и непрерывные в области G: <H и обладающие в этой области непрерывными частными производными по всем своим аргументам.

Функция V(x1,…,xn) называется знакоположительной (знакоотрицательной) в указанной области G, если для любого .

Функция V(x1,…,xn) называется положительно определенной (отрицательно определенной) в той же области G, если для любого , причем тогда и только тогда, когда =0.

Функции V (x1,…,xn) первого типа называют знакопостоянными, второго типа – знакоопределенными.

Достаточно просто определяется знакоопределенность в том случае, если функция V(x1,…,xn) представляет собой квадратичную форму, то есть

.

Тогда функция V (x1,…,xn) является положительно определенной, если положительно определена вышеуказанная квадратичная форма.

Дадим знакоопределенной функции V(x1,…,xn) геометрическую интерпретацию. Рассмотрим функцию двух переменных V(x1,x2). На плоскости x1, x2 линия V(x1,x2)=с (c – некоторое число) представляет собой замкнутую кривую, содержащую внутри себя начало координат (рис. 3). При c=0 кривая стягивается в начало координат.

Пусть si(t) – некоторое решение системы (1), удовлетворяющее начальным условиям si(t0)=xi0.

Полной производной по времени t функции V(x1,…,xn) в силу системы (1) называется функция

,

или, учитывая формулу полной производной,

.

Из этой формулы следует, что производная в силу системы (1) не зависит от выбранного решения s(t), а является функцией точки . Иначе полученное выражение можно записать так:

.

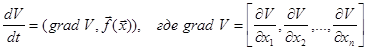Производная представляет собой скалярное произведение вектора на вектор фазовой скорости . При >0 фазовые траектории системы (1) пересекают поверхность в сторону возрастания , а при <0 – в сторону убывания.

Положительно определенные функции , производные которых в силу системы (1) являются отрицательно определенными или знакоотрицательными, называются функциями Ляпунова.

Теорема Ляпунова об устойчивости гласит, что если для системы уравнений (1) существует положительно определенная функция , производная которой в силу системы (1) знакоотрицательна, то тривиальное решение системы (1) устойчиво по Ляпунову .

Пусть для системы дифференциальных уравнений (1) существует положительно определенная функция , производная которой в силу системы (1) отрицательно определена. Теорема Ляпунова об асимптотической устойчивости гласит, что тогда тривиальное решение системы (1) асимптотически устойчиво по Ляпунову.