Реферат: Теория устойчивости систем

Рассмотрим вспомогательную систему уравнений:

. (5)

Пусть определитель этой системы не равен нулю:

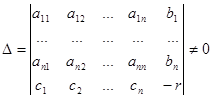. (6)

В этом случае эта система уравнений имеет единственное решение, которое мы найдем по правилу Крамера:

(7)

.

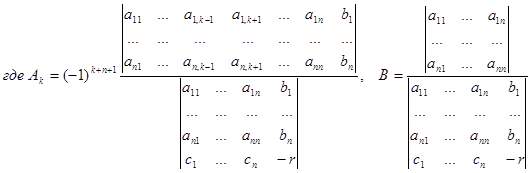Если a2=0, то из второго уравнения системы (4) следует, что e=0, и, согласно равенствам (7) получаем xk=0 ( k=1,…,n) и y=0. Таким образом, система дифференциальных уравнений (1)–(3) имеет единственное состояние равновесия с координатами

xk=0, y=0 (k=1,…,n). (8)

Если a2¹0, то система уравнений (4) может иметь несколько решений. Из (7) и (4) следует

(9)

Это уравнение может иметь различные решения в зависимости от знака величины Ba 2 и формы кривой f(e). Если Ba2<0, то уравнение (9) имеет единственное решение e=0, и система уравнений (4) имеет решение (8). Если Ba2>0, то уравнение (9) может иметь несколько решений. Обозначим их e1, …, em; тогда система (4) имеет m решений, определяемых равенствами

xki=Akei (k=1,…,n), yi=Bei (i=1,…,m). (10)

Таким образом, в зависимости от вида нелинейной функции f(e) и значений a2 и B в САР возможны следующие виды состояния равновесия:

1) Единственное состояние равновесия (8);

2) Конечное число состояний равновесия (10).

Исследование устойчивости любого из состояний равновесия (10) может быть сведено к рассмотрению устойчивости тривиального решения (8).

Пусть a1=1, a2=0. Тогда

. (11)

Исследование устойчивости тривиального решения системы (11) удобно проводить, когда уравнения приведены к канонической форме. Канонической формой уравнений (11) назовем такой их вид, когда матрица A приведена к жордановой форме. Для любой числовой матрицы A существует такая невырожденная матрица T, что T­-1AT=J, где J – жорданова форма матрицы A.

Сделаем в системе (11) замену переменных:

Тогда из (11):

или .

Пусть , тогда

. (12)

Эта система уравнений является канонической формой уравнений движения. Мы рассматриваем случай простых корней характеристического уравнения матрицы A, поэтому J=diagA.

Для того, чтобы состоянию равновесия xk=0, y=0 системы уравнений (11) соответствовало единственное состояние равновесия zk=0, e=0 последней системы уравнений, требуется, чтобы определитель системы (12) был отличен от нуля, то есть