Реферат: Теория устойчивости систем

Характеристическое уравнение:

.

Его корни: l 1=l2=–1.

Оба корня лежат в левой полуплоскости, значит, тривиальное решение системы устойчиво.

9. Исследование устойчивости линейных систем с помощью второго метода Ляпунова.

Рассмотрим линейную стационарную систему:

(1)

Пусть положение равновесия этой системы будет находится в точке . Будем искать функцию Ляпунова в виде:

Рассмотрим производную этой функции в силу уравнения (1):

.

Мы получили также квадратичную форму. Поэтому чтобы производная по времени от функции Ляпунова была отрицательно определенной, эта квадратичная форма должна быть отрицательно определенной. Обозначим:

.

Зададим матрицу G как некоторую положительно определенную матрицу. Тогда мы получим уравнение относительно матрицы H, называемое уравнением Ляпунова.

Если матрица H, найденная из этого уравнения, является положительно определенной матрицей, то система устойчива, в противном случае система неустойчива.

10. Исследование устойчивости нелинейных систем с помощью второго метода Ляпунова

Рассмотрим анализ устойчивости состояния равновесия некоторого класса нелинейных систем автоматического регулирования с помощью второго метода Ляпунова. Полагаем, что нелинейная САР состоит из линейного объекта регулирования и нелинейного регулятора. Поведение объекта регулирования описывается линейной системой дифференциальных уравнений с постоянными коэффициентами, которая в векторной записи имеет вид:

, (1)

где 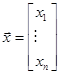– вектор координат, характеризующих состояние объекта регулирования;

y – скалярная координата, характеризующая воздействие регулятора на объект регулирования (регулирующее воздействие).

Матрица А полагается невырожденной (detA

Регулятор имеет в своём составе сервомеханизм, управление которого

(2)

и чувствительный момент, формирующий сигнал ошибки

, (3)

где – вектор постоянных коэффициентов; r – скалярный параметр обратной связи. Относительно нелинейной функции будем полагать, что , если e ¹0. В точке e=0 допускается разрыв непрерывности первого рода, функция f(e) предполагается непрерывной при e¹0.

Введем следующую классификацию рассматриваемых нелинейных САР в зависимости от характера корней характеристического уравнения матрицы A. САР будет:

1) собственно устойчива, если все корни характеристического уравнения матрицы A имеют отрицательные вещественные части, то есть Reli<0;

2) нейтральна по координатам x1,…,xk, если Rel1=Rel2=…=Relk=0, а остальные корни имеют отрицательные вещественные части;

3) собственно неустойчива, если хотя бы один корень характеристического уравнения имеет положительную вещественную часть.

Рассмотрим случай, когда корни характеристического уравнения матрицы A простые и удовлетворяют условию Reli≤0, i=1,2,…,n. Определим состояния равновесия, которые могут быть в нелинейной САР, описываемой уравнениями (1)–(3). Эти состояния равновесия представляют собой решения системы линейных алгебраических уравнений