Реферат: Уравнения с параметрами

-3 -2 0 1 2 а

В соответствии с этой иллюстрацией при а= — 3 получаем х = — 3 — 3= — 6;

при a = — 2 х = — 2 — 3= — 5; при a =1 х = 1+1=2; при a=2 х =2+1=3.

Итак, можно записать

От в ет: 1) если a = — 3, то х = — 6; 2) если a = — 2, то х = — 5; 3) если a =0, то корней нет; 4) если a = l, то х =2; 5) если а=2, то х =3;

6) если а ≠ -3 ;

а ≠ -2 ;

а ≠ 0 ; то х ₁ = а + 1,

а ≠ 1 ; х ₂ = а – 3.

а ≠ 2,

Иррациональные уравнения с параметрами.

Существует несколько способов решения иррациональных уравнений с параметрами. Познакомимся с ними, разобрав следующий пример.

П р и м ер . Решить уравнение х - = 1. (6)

Решение:

Возведем в квадрат обе части иррационального уравнения с последующей проверкой полученных решений.

Перепишем исходное уравнение в виде:

= х – 1 (7)

При возведении в квадрат обеих частей исходного уравнения и проведения тождественных преобразований получим:

2 х ² – 2х + (1 - а ) = 0, D = 2а – 1.

Особое значение : а = 0,5. Отсюда :

1) при а > 0,5 х _1,2 = 0,5 ( 1 ± );

2) при а = 0,5 х = 0,5 ;

3) при а <0,5 уравнение не имеет решений.

Проверка:

1) при подстановке х = 0,5 в уравнение (7), равносильное исходному, получим неверное равенство. Значит, х = 0,5 не является решением (7) и уравнения (6).

2) при подстановке х₁ = 0,5 ( 1 ± ) в (7) получим:

-0,5 ( 1 + ) = – ( 0,5 ( 1 - ))²

Так как левая часть равенства отрицательна, то х₁ не удовлетворяет исходному уравнению.

3) Подставим х ₂ в уравнение (7):

=

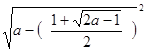Проведя равносильные преобразования, получим:

Если , то можно возвести полученное равенство в квадрат: