Реферат: Уравнения с параметрами

Имеем истинное равенство при условии, что

Это условие выполняется, если а ≥1. Так как равенство истинно при а ≥1, а х₂ может быть корнем уравнения (6) при а > 0,5, следовательно, х₂ – корень уравнения при а ≥1.

Тригонометрические уравнения.

Большинство тригонометрических уравнений с параметрами сводится к решению простейших тригонометрических уравнений трех типов. При решении таких уравнений необходимо учитывать ограниченность тригонометрических функций у = sinx и y = cosx. Рассмотрим примеры.

Пример . Решить уравнение: cos =2а .

Решение: Так как Е (соst )=[-1; 1], то имеем два случая.

1. При |a | > 0,5 уравнение не имеет решений.

2. При |a | ≤0,5 имеем:

а ) =arccos2a+2πn. Так как уравнение имеет решение, если arccos2а +2π n ≥0, то n может принимать значения n =0, 1, 2, 3,.... Решением уравнения является х = 1+(2π n +аrссоs2а )²

б) =-аrссоs2а +πn . Так как уравнение имеет решение при условии, что -аrссоs2а +2πn >0, то n =1, 2, 3,..., и решение уравнения. х =1+(2πn -arccos2a )² .

Ответ: если |a | > 0,5, решений нет;

если |a | ≤0,5 , х = 1+(2π n +аrссоs2а )² при n = 0, 1, 2,... и х =1+(2πn -arccos2a )² при n N.

Пример . Решить уравнение: tgax ² =

Решение: .

ах ² = +π n , n Z

Если коэффициент при неизвестном зависит от параметра, то появляется особое значение параметра. В данном случае:

1. Если а =0, то уравнение не имеет решений.

2. Если а 0, то х ² = , n Z

Уравнение имеет решение, если ≥0. Выясним, при каких значениях n

и а выполняется это условие:

≥0

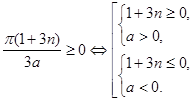
откуда n ≥ и а > 0 или n ≤ и а < 0.

Итак, уравнение имеет решение х = ± , если

1) а > 0 и n = 1,2,3,… или

2) а < 0 и n Z .

Ответ: при а = 0 решений нет;

при а > 0 и n = 1,2,3,… или а < 0 и n Z х = ± .

Пример. Решите уравнение: а sinbx = 1

Решение: Особое значение параметра а : а = 0.

1. При а = 0 решений нет.