Шпаргалка: Дискретная техника

Растровое кодирование.

Понятие «растр изображения»

Если рассмотреть с помощью увеличительного стекла черно-белое графическое изображение, напечатанное в газете, то можно увидеть, что оно состоит из мельчайших точек, образующих характерный узор. Узор этот называется растром. Размеры и яркость каждой точки можно выразить с помощью целых чисел и таким образом осуществить кодирование растра с использованием цифрового (двоичного) кода.

Для черно-белых иллюстраций принято представление в виде комбинации точек с 256 оттенками серого цвета, для чего достаточно 8-разрядного двоичного кода.

Векторное кодирование

Понятие «графический примитив».

Некоторые виды изображений проще представить в виде набора простейших геометрических фигур: кругов, квадратов, овалов, кривых и прямых линий. Для изображения каждого из этих элементов (их ещё называют графические примитивы) необходимо указать только некоторые основные параметры.

Пример: Для изображения окружности достаточно заказать её центр, длину радиуса и, возможно, толщину линии обводки. Для изображения квадрата достаточно указать координаты верхнего левого, и нижнего правого углов, и толщину линию обводки. , Кривые линии могут быть построены с использованием множества уравнений кривых второго порядка (y=ax2+bx1+c), кривых третьего порядка (у=ах3+Ьх2+сх+а) и кривых Безье.

Такой способ кодирования фигур и изображений позволяет сократить количество данных, необходимых для их описания.

Каждый из двух описанных выше способов кодирования графической информации имеет свои недостатки и преимущества и находит своё применение в различных областях. Растровое кодирование чаще применяется при работе с фотографиями, или какими-либо другими изображениями, на которых трудно выделить регулярные формы. Векторное кодирование находит широкое применение при создании всевозможных чертежей, схем и логотипов

Кодирование звуковой информации

Понятия «звуковой синтез» и «волновая таблица».

При кодировании звука в ЭВМ используется несколько методов. Рассмотрим наиболее распространённые из них: метод частотной модуляции и метод таблично-волнового синтеза.

Метод частотной модуляции. Основан на том, что теоретически любой сложный звук можно разложить на последовательность простейших гармонических сигналов разных частот, каждый из которых представляет собой правильную синусоиду, а следовательно может быть описан числовыми параметрами, т. е. кодом.

В природе звуковые сигналы имеют непрерывный спектр, то есть являются аналоговыми. Их представление в виде дискретных цифровых сигналов выполняют специальные устройства - аналогово-цифровые преобразователи (АЦП). Обратное преобразование для воспроизведения звука, закодированного числовым кодом, выполняют цифро-аналоговые преобразователи (ЦАП).

Метод таблично-волнового синтеза. Этот метод упрощённо можно охарактеризовать так: в ЭВМ в заранее подготовленных таблицах хранятся образы звуков для множества различных музыкальных инструментов. Числовые коды выражают тип инструмента, номер его модели, высоту тона, продолжительность звучания и другие параметры. Звук, воспроизводимый в ЭВМ, получается в результате синтеза отдельных звуков в специальном устройстве - синтезаторе. Такой синтезатор является неотъемлемой частью всех современных электронных устройств воспроизведения звука, входящих в состав компьютеров и именуемых «звуковой картой».

Логические схемы и основы алгебры логики

Все устройства ЭВМ состоят из элементарных логических схем. Работа этих схем основана на законах и правилах алгебры логики, которая оперирует двумя понятиями: истинности и ложности высказывания. В соответствии с такой двоичной природой высказываний их условились называть логическими двоичными переменными и обозначать «1» в случае истинности (true) и «0» в случае ложности (false).

Две логические переменные X1 и X2, принимающие независимо друг от друга значения «0» и «1», могут образовывать логические функции. Всего, для двух независимых переменных, можно составить 16 различных функций. Рассмотрим некоторые из них.

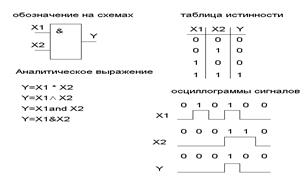
Логическое умножение «И»

- логическое умножение двух переменных Х1 и Х2 есть логическая функция Y, которая истинна только тогда, когда одновременно истинны обе входные переменные.

Логическое сложение «ИЛИ»

- логическое сложение двух переменных X1 и X2 это логическая функция Y, которая истинна, когда хотя бы одна из входящих переменных истинна.

-

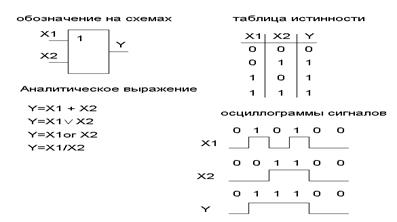
Логические функции часто характеризуют таблицей истинности.

Таблица истинности – это таблица соответствия всех возможных комбинаций входных логических переменных и соответствующей им выходной логической функции.

Логическое отрицание «НЕ»

- логическое отрицание переменной Х это логическая функция Y, которая истинна только тогда, когда Х ложно и, наоборот, ложна тогда, когда Х истинна.