Шпаргалка: Дискретная техника

Три рассмотренные функции позволяют реализовать любую логическую зависимость. На основе их строятся более сложные логические функции.

Функция «ИЛИ-НЕ» (операция стрелка Пирса)

- функция обратная к «ИЛИ»

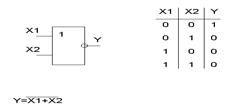
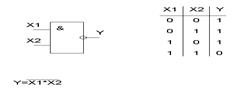
Функция «И-НЕ» - (операция штрих Шеффера)

- функция обратная к «И»

-

Функционально полная система логических элементов – это такой набор элементов, используя который можно реализовать любую сколь угодно сложную логическую функцию.

Ввиду того, что любая логическая функция представляет собой комбинацию простейших функций «И», «ИЛИ» и «НЕ», то набор этих элементов является функционально полным.

То же самое можно сказать и об элементах, реализующих функции «И-НЕ»и «ИЛИ-НЕ». Каждый из них является функционально полным, то есть в любом из них может быть реализована любая логическая функция.

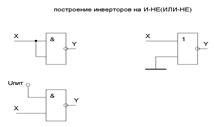
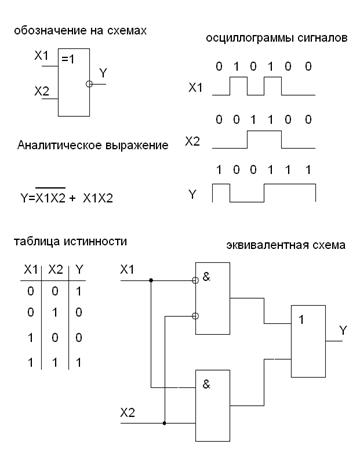
Исключающее «ИЛИ» (сумма по модулю 2 – операция XOR)

- суммой по модулю 2 двух переменных X1 и X2 является логическая функция Y, которая истинна только тогда, когда одна из входных переменных истинна, а другая ложна.

(Эта функция реализует операцию неравнозначности).

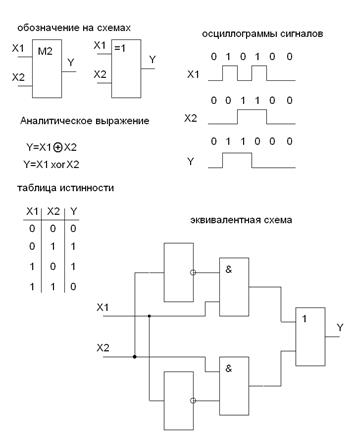
Схема равнозначности

- логическая функция Y истинна, только тогда, когда обе входные переменные X1 и X2 равнозначны, то есть либо одновременно «ложны», либо одновременно «истинны»

Синтез логических схем

«Отличие науки от искусства заключается в том, что наука базируется на формализованных методах решения однотипных задач».

Множество состояний комбинационного устройства может быть охарактеризовано функцией алгебры логики (ФАЛ), которая описывает входные и выходные состояния этого устройства.

ФАЛ может быть задана в виде:

- словесного описания;

- таблицы истинности;

- числовой последовательности;

- аналитического выражения.

Пример: Функция алгебры логики задана в виде числовой последовательности:

Y={3,6,7}#10x1x2x3