Шпаргалка: Дискретная техника
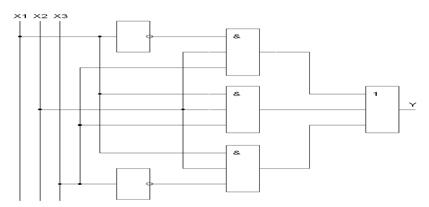
Таблица истинности такой функции выглядит так:
| X1 | X2 | X3 | Y |
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 |
| 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 |
Запишем логическое выражение для этой функции:
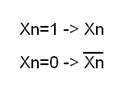
Для этого для каждого состояния «Y=1» запишем логическое произведение переменных по правилу если Xn=1, то в произведение запишем его прямое значение; если Xn=0, то в произведение запишем его инверсное значение.
Записанные логические произведения объединим логической суммой.
Полученное выражение будет иметь следующий вид:
Для схемотехнической реализации полученной логической функции потребуется три трехвходовых схемы И, одна трехвходовая схема ИЛИ и два инвертора НЕ.
Правила алгебры логики позволяют преобразовать полученное выражение к более простому и удобному виду:
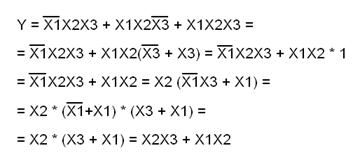
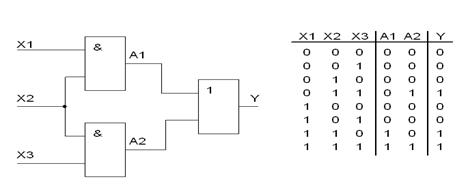Для практической реализации этой функции потребуется два двухвходовых элемента «И» и один двухвходовой элемент «ИЛИ».
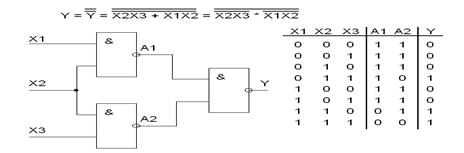
Применив правило де-Моргана, можно преобразовать выражение к виду, удобному для реализации схемы на других элементах.
Допустим, что для построения схемы мы можем использовать только элементы И-НЕ, тогда:
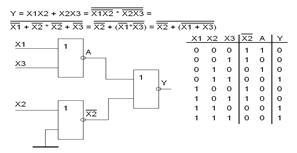
Допустим, что мы можем использовать только элементы ИЛИ-НЕ, тогда:
Комбинационные и последовательностные устройства
Все устройства, оперирующие с двоичной (дискретной) информацией, подразделяются на два больших класса: комбинационные схемы (дискретные автоматы без памяти) и последовательностные устройства (дискретные автоматы с памятью).
Комбинационные схемы.
Комбинационной схемой или логическим устройством называют такое устройство, у которого сигналы на выходах в любой момент времени однозначно определяются сочетанием сигналов на входах и не зависят от предыдущих состояний данного устройства.
Схемным признаком таких устройств служит отсутствие цепей обратной связи, то есть замкнутых петель для прохождения сигналов с выходов устройства на его входы.
Примером комбинационных схем могут служить отдельные логические элементы, наборы электронных ключей, шифраторы, дешифраторы, мультиплексоры, демультиплексоры и большинство арифметических устройств: сумматоры, полусумматоры, перемножители и т.д.
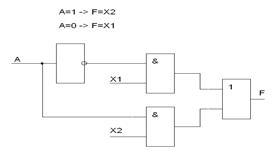
Мультиплексоры.
Назначение мультиплексора – коммутация в желаемом порядке информации, поступающей с нескольких входных линий на одну выходную.
С помощью мультиплексора осуществляется разделение во времени информации, поступающей по разным каналам. Мультиплексор можно рассматривать как бесконтактный многопозиционный переключатель.
Мультиплексор «два к одному».
Для переключения входных сигналов используется один внешний сигнал.
