Шпаргалка: Интегралы, дифуры, матрицы

Мінори та алгебраїчні доповнення. Визначник n-ого порядку.

Мінором k-того порядку kє [1; n-1] називається визначник утворений з елементів, які стоять на перетені будь-яких k рядків і k товпчиків визначника.

Алгебраїчним доповненням до мінора k-того порядку є доповнювальний мінор (n-k)-того порядку, взятий із знаком , де

Якщо - сума номерів і стовпчиків - парна, то знак “+”, якщо не парна, то знак “-“.

Означення: Визначником n–ого порядку називається число, яке дорівнює алгебраїчній сумі добутків елементів будь-якого рядка, або стовпчика на відповідні їм алгебраїчні доповнення.

Правило Крамера.

Якщо головний визначник, складений з коефіцієнтів при невідомих, системи n-лінійних рівнянь з n-невідомими відмінний від нуля, то така система рівнянь має єдиний розв’язок (сумісна і визначена), який знаходиться за формулами:

, , ...,.

де -головний визначник, який складається з коефіцієнтів при невідомих у лівій частині системи.

-визначник, який одержується шляхом заміни j-го стовпчика в головному визначник на стовпчик вільних членів.

Оберненна матриця.

Матриця називається оберненною матрицею для квадратної, невиродженної А, якщо виконується співвідношення: .

Оберенні матриці існують для квадратних не особливих матриць.

Розв’язування систем рівнянь за допомогою оберненної матриці.

Знаходять обернену матрицю таким чином:

1.

2. Алгебрарічні доповнення , до всіх елементів матриці А.

3. З алгебрарічнихдоповнень сскладають матрицю в яку записують алгебраїчні доповнення не в звичайному порядку, а в транспоновану -

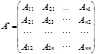
4.

N-вимірний векторний простір.

Сукупність впорядкованих систем з n-дійсних чисел, для яких означені дії додавання і множення на число, утворює n-вимірний векторний простір.

Елементами означенного таким чином простору будуть впорядковані системи чисел, які називаємо n-вимірними вектороми.

Лінійна залежність та незалежність векторів. Ранг сукупності векторів.

Система векторів називається лінійною залежною, якщо існують такі числа

хоча б одне з яких відмінне від нуля, що має місце рівність:

(1)

Якщо рівність (1) можлива лише у випадку, коли всі то система векторів називається лінійно незалежною.

Кількість векторів, що входять в будь-яку максимальну, лінійну незалежну підсистему даної системи векторів, називаюється рангом цієї системи.