Статья: Об одной общей краевой задаче со смещением для нагруженного уравнения третьего порядка с кратными характеристиками
Пусть имеет место случай (1) и функции ![]() . Решение задачи (6), (7) в этом случае имеет вид:
. Решение задачи (6), (7) в этом случае имеет вид:
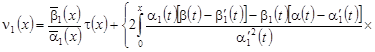
![]()
![]() , (8)
, (8)
где 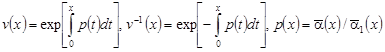 .
.
Дифференцируя равенство (8) и делая несложные преобразования, получаем:
![]()
![]() (9)
(9)
где ![]() ,
,
![]() ,
, 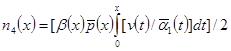 ,
,
![]() ,
,
![]()
![]() ,
, ![]() .
.
Переходя к пределу в уравнении (1) при ![]() , получаем функциональное соотношение между
, получаем функциональное соотношение между ![]() и
и ![]() , принесенное из области
, принесенное из области ![]() , на линию
, на линию ![]() :
:
![]() . (10)
. (10)
В силу граничных условий (2) и равенства (9) получим нелокальную задачу для нагруженного неоднородного интегро-дифференциального уравнения третьего порядка с переменными коэффициентами:
![]() , (11)
, (11)
![]() , (12)
, (12)
где ![]()
![]() .
.
В начале положим, что ![]() , т.е.
, т.е.
![]() ,
, ![]() , т.е.
, т.е.
![]() .
.
В зависимости от значений корней характеристического уравнения
![]() , (13)
, (13)
соответствующего однородному уравнению (11) (![]() ), будем исследовать разрешимость задачи (11), (12).
), будем исследовать разрешимость задачи (11), (12).
Введем обозначение ![]() . Логически возможны три различных случая: 1) S>0, 2) S=0, 3) S<0.
. Логически возможны три различных случая: 1) S>0, 2) S=0, 3) S<0.
Известно, что [2]: 1) если S>0, то уравнение (13) имеет только один действительный корень, а два остальных корня будут сопряженными чисто комплексными числами; 2) если S=0, то все три корня уравнения (13) действительны, причем два из них равны; 3) если S<0, то все три корня уравнения (13) действительны, причем все они различны.
Пусть S=0, т.е. ![]() .
.