Статья: Об одной общей краевой задаче со смещением для нагруженного уравнения третьего порядка с кратными характеристиками
Рассмотрим линейное нагруженное уравнение третьего порядка:
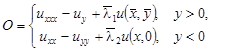(1)
в – области 
, ограниченной отрезками 
прямых 
соответственно при 
и характеристиками 
, 
уравнения (1) при ; 
; 
– интервал 
, 
– интервал 
.
Здесь положено, что:
1) 
или 2) 
.
Пусть имеет место случай (1).
Задача 
. Найти функцию 
со следующими свойствами: 1) 
;
2) 
– регулярное решение уравнения (1) при 
;
3) 
удовлетворяет краевым условиям
, 
; (2)
,
, (3)
где 
, 
– аффиксы точек пересечения характеристик уравнения (1) при y < 0, выходящих из точки 
с характеристиками АС и ВС соответственно; 
, 
, 
.
Опираясь на однозначную разрешимость задачи Коши для уравнения (1) при y < 0 с начальными данными 
, 
, легко видеть, что если существует решение задачи , то оно представимо в виде:
. (4)
Учитывая (4) в краевом условии (3), получаем:
, (5)
где 
.
Следуя [1], обозначим через 
первообразную функции 
. Тогда уравнение (5) примет вид:
, (6)
, (7)
где 
.
Относительно коэффициентов уравнения (6) будем рассматривать аналогичные ситуации, приведенные в работе [1]:
1) 
, т.е. 
;
2) 
, , т.е. 
;
3), т.е. 
;
--> ЧИТАТЬ ПОЛНОСТЬЮ <--