Статья: Об одной общей краевой задаче со смещением для нагруженного уравнения третьего порядка с кратными характеристиками

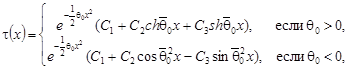
где .

Пусть . Методом вариации постоянных находим общее решение неоднородного уравнения (34) в виде:

, (35)

где ,

.

Удовлетворяя (35) условиям (12), получаем:

,

,

где

,

,

, причем выполняется условие

, т.е. .

Равенство (35) перепишем в виде:

, (36)

где , .

Из (36) при , имеем

,

если выполняется условие , т.е.

.

Пусть имеет место случай 3), причем , . Тогда уравнение (6) принимает вид [1]:

. (37)

Полагая в равенстве (37) и, учитывая условия , получим:

.

Следовательно, для имеем представление

, (38)

где .