Учебное пособие: Четырехполюсники, электрические фильтры

- действительная часть;

- мнимая часть.

Уравнение (2.16) запишем в виде:

(2.17)

Фазочастотная характеристика ФНЧ-2 определяется по формуле:

(2.18)

Комплексная передаточная функция по напряжению определяется из (2.17):

(2.19)

Модули передаточных функций по напряжению и мощности принимают вид:

(2.20)

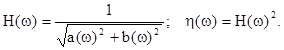
Таким образом, при известных значениях R, L, C-элементов, по формулам (2.18), (2.20) можно рассчитать и построить графики АЧХ и ФЧХ Г-образного ФНЧ.

С целью общего анализа частотных характеристик Г-образного ФНЧ представим передаточные функции (2.20) в параметрической форме, для чего обозначим:

- приведенная (нормированная) частота; - резонансная частота; - сопротивление индуктивности; - проводимость емкости; - волновое (характеристическое) сопротивление; - коэффициент нагрузки.

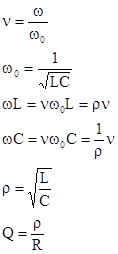
После подстановки обозначений в (2.20) получим передаточные функции в параметрической форме:

(2.21)

Пример 2.3. Рассчитать и построить семейство кривых передаточной функции по мощности в параметрической форме для трех значений коэффициента нагрузки:

Определить коэффициент прямоугольности передаточной функции по мощности при

Расчет передаточной функции по мощности, выполненный по формуле (2.21) приведен на Рис.2.9.

Из Рис.2.9 следует, что при Q₁ =0,8 передаточная функция достигает своего максимума, равного 1,86, а затем плавно уменьшается, Этот всплеск передаточной функции может быть желательным или нежелательным в зависимости от конкретного назначения фильтра.

При Q₂ =1 всплеск передаточной функции значительно меньше и при он вовсе отсутствует.

Таким образом, характер изменения передаточной функции Г-образного ФНЧ целиком определяется значением коэффициента нагрузки Q, который, в свою очередь, зависит от комбинации значений RLC-элементов. Следовательно, путем соответствующего выбора LC-элементов можно изменить форму кривой передаточной функции.