Учебное пособие: Четырехполюсники, электрические фильтры

где - граничная частота, на которой реактивное сопротивление емкости равно активному сопротивлению

Запишем (2.9) и (2.10) в параметрической форме:

(2.12)

(2.13)

Параметрические функции (2.11) и (2.12) позволяют проводить общий анализ АЧХ и ФЧХ фильтра при заданных значениях R, r-элементах и произвольном значении емкости С.

Пример 2. Рассчитать и построить графики при следующих исходных данных:

R=100 Ом – сопротивление нагрузки;

r=5 Ом – внутреннее сопротивление источника.

Оценить коэффициент прямоугольности передаточной функции по мощности.

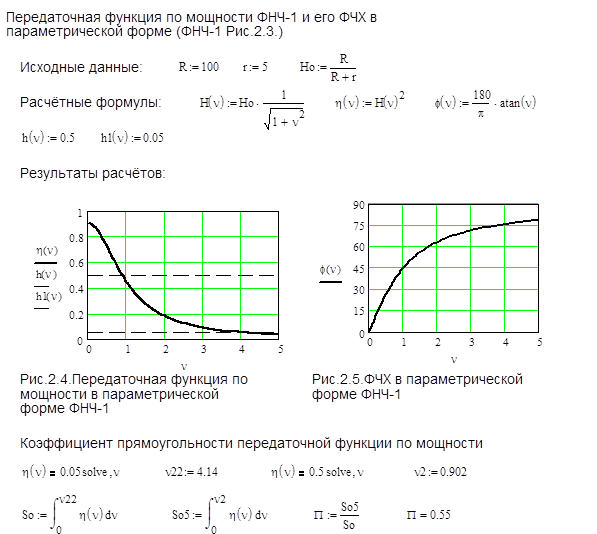
Результаты расчетов представлены на Рис.2.4 и Рис.2.5.

Из этих рисунков видно, что передаточная функция по мощности при частоте ν=0 принимает значение H(0)=0,98, а затем плавно уменьшается с увеличением частоты. Коэффициент прямоугольности этой функции составляет всего П=0,545. Это означает, что данный фильтр соответствует идеальному фильтру на 54,5%.

Сдвиг фаз между входным и выходным напряжениями изменяется от 0 до 90⁰ . При этом выходное напряжение опережает входное.

2.4.2 Синтез емкостного фильтра нижних частот первого порядка

Синтез (проектирование) любого технического устройства начинается с разработки технического задания (ТЗ), в котором приводятся исходные данные и формулируются требования к устройству.

Применительно к ФНЧ-1 техническое задание на его проектирование можно изложить следующим образом:

1. Спроектировать емкостной фильтр нижних частот, схема которого приведена на Рис.3.2.

2. На вход фильтра подаются сигналы синусоидальной формы, частота которых изменяется от 0 до ∞.

3. Сопротивление нагрузки R, а внутреннее сопротивление источника r, (R>>r).

4. Передаточная функция по напряжению на нижней границе полосы пропускания (f₁ =0) должна принимать значение, близкое к единице, а на верхней границе f₂ передаточная функция должна принимать значение H(f₂ )=H₁ .

5. Определить потребное значение емкости, рассчитать АЧХ и ФЧХ фильтра, оценить коэффициент прямоугольности передаточной функции по мощности.

В условиях данной задачи неизвестной величиной является только емкость, которую достаточно просто можно найти из уравнения передаточной функции. Однако, в интересах общности изложения последующего материала воспользуемся передаточной функцией в параметрической форме (2.14), из которой найдем значение приведенной частоты n₂ , на которой передаточная функция (2.12) принимает заданное значение H₁ :

(2.14)

Очевидно, что (2.14) имеет смысл только при H₁ <H₀ .

Теперь формулу (2.11) можем записать в виде

откуда находим потребное значение емкости для построения ФНЧ-1 Рис.3.2:

(2.15)

Пример 2.2. Спроектировать ФНЧ-1 Рис.2.3 при следующих исходных данных:

R=100 Ом – сопротивление нагрузки;

r=5 Ом – внутреннее сопротивление источника;