Как видно из таблицы конечных разностей при увеличении порядка конечных разностей ошибка в исходных данных распространяется и растет.

Такое взаимодействие ошибок называют шумом, если это ошибки округлений - то шумом округлений .

Если ошибки округлений достаточно большие, то может происходить следующее явление: при увеличении порядка конечных разностей они могут уменьшаться и→0, но, дойдя до некоторого малого значения, опять могут начать расти из-за шума округлений.

Столбец в таблице конечных разностей, в которой все конечные разности ≈0, называют «практическим постоянным»; при этом конечные разности высших порядков не используют.

Для интерполяции целесообразно использовать многочлен такой степени, которая совпадает с порядком «практической постоянной» конечных разностей.

ЛЕКЦИЯ №8

ИНТЕРПОЛЯЦИОННАЯ ФОРМУЛА НЬЮТОНА ДЛЯРАВНООТСТОЯЩИХ УЗЛОВ

Дана функция y=¦(c),заданная на сетке равноотстоящих узлов:

y_i =¦(c_i ), x_i =x₀ +ih_i ,

Строим интерполяционный полином с целью упрощения записи полинома (интерполяционного) и представления его в виде, позволяющем оценивать влияние каждого из компонентов на значение аппроксимации, запишем его так:

N_n (x)=-a₀ +a₁ (x-x₀ )+a₂ (x-x₀ )(x-x₁ )+…+a_n (x-x₀ )…(x-x_n-1 ) (8.1)

Необходимо посчитать его коэффициенты a_i . Будем находить из условия

N_n (x_i )=y_i

i=0 : N_n (x₀ )=y₀ =a₀ +a₁ 0+…+a_n 0 a₀ = y₀

i=1 : N_n (x₁ )=y₁ = y₀ +a₁ (x₁ -x₀ ) + a₂ 0+…+a_n 0

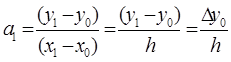
x₁ =x₀ +1h=x₁ -x₀ =h

i=2 : N_n (x₂ )=y₂ = y₀ +∆y₀ /h(x₂ -x₀ ) (x₂ -x₁ ) + a₃ 0+…+a_n 0

x₂ -x₀ =2h

x₂ -x₁ =h

y₂ = y₀ +∆y₀ 2+a₂ 2h²

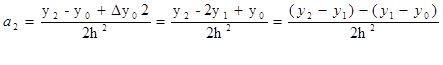
i = k : (8.2)

Запишем теперь, используя (8.2) , полином (8.1) в виде:

N_n (x)= y₀ +∆y₀ /h(x-x₀ )+…+ ∆ⁿ y₀ /n!hⁿ (x-x₀ )(x-x₁ )… (x-x_n-1 ) (8.3)

Полином (8.3) 1-ый интерполяционный многочлен Ньютона. Он наиболее приспособлен для вычисления значения функции в точках, близких к x₀

С целью упрощения записи полинома введем переменную

x=x₀ +gh

Если g-целое, то будет совпадать с номером узла

x₀ – базовый узел полинома (8.3)