Учебное пособие: Численные методы

МЕТОДЫ РЕШЕНИЯ СИСТЕМ НЕЛИНЕЙНЫХ УРАВНЕНИЙ

СНУ

Пусть дана система вида:

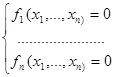(5.1)

f'(x)=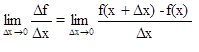 - производная

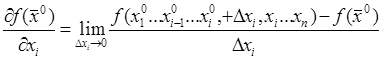
Частная производная - вектор (все значения).

МЕТОД НЬЮТОНА

Дана система вида (5.1), где f_i один раз непрерывно дифиринцируемые функции, т.е. существуют все частные первые производные этих функций.

Строим последовательность приближений сходящуюся к точному решению системы .

Пусть - некоторое начальное приближение к решению, а - катое приближение к решению. Построим зависимость, позволяющую на основании построить .

Точное приближение

ξ-корень обращает уравнение в верное равенство(тождество).

(5.2)

Разложим функции f_i из системы (5.2) в ряд Тейлора в окрестности точки х^к до линейных составляющих.

(5.3)

Система (5.3) представляет собой систему линейных алгебраических уравнений для поиска компонента вектора поправки h^k .

Перепишем систему (5.3) в виде:

(5.4)

Сокращаем запись системы (5.4) : (5.5)

Решим систему (5.5) методом обратной матрицы. Определитель Якобиана в точке х^к не равен 0.

Получили связь последующего приближения с предыдущим.

(5.6)

условие окончания вычислений. (5.7)

- расстояние между векторами (метрика).

МЕТОД ИТЕРАЦИЙ

--> ЧИТАТЬ ПОЛНОСТЬЮ <--