Учебное пособие: Численные методы
Nn (g)= y0 +∆y0 g+…+ ∆n y0 /n!g(g-1)(g-2)(g-n+1) (8.4)
Полином Ньютона в силу единственности существования интерполяционного полинома Лагранжа является одной из форм записи полинома Лагранжа, поэтому для полинома (8.3) справедливо, что формула остаточного члена полинома Лагранжа
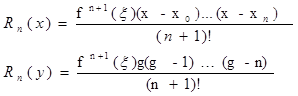
Для вычисления функции в точках находящихся в середине сетки узлов интерполяции либо в ее конце, т. е близкие к xn , применяют два подхода
1. строят формулы для вычисления функции в точках х, близких к середине сетки интерполяции
2. формулы для точек х, близких к хn (упорядочивание узлов интерполяции).
Соответственно получаются формулы Стирлинга , Бесселя, Гаусса, и 2-ой интерполяционный многочлен Ньютона .
Второй путь: в качестве узла х0 для заданной точки х берут тот узел, который наиболее близок к х, узел х1 выбирают как самый близкий из оставшихся узлов к х.
Т.е последовательность 
упорядочившаяся по возрастанию.
Для вычисления значения функции в точке х используется 1-ый интерполяционный многочлен Ньютона.
 |
х0 х1 х2 х3 х4 х5 х6
Преобразуем узлы:
х0 ′=x3;
x1 ′=x4 ;
x2 ′=x2 ;
x3 ′=x5 ;
Разделенные разности
Пусть функция ¦(c),задана на системе неравно отстоящих узлов.
Разделенной разностью 1-го порядка назовем выражение:
Разделенной разностью 2-го порядка:
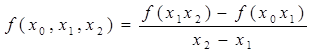
Разделенной разностью k-го порядка:
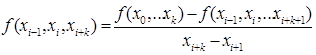(8.6)
|x-x0 |, 
Свойства разделенной разности:
- на сетке равноотстоящих узлов разделенной разности совпадают конечными разностями
- разделенные разности понижают степень многочлена
- разделенные разности n-го порядка постоянны и равны
Интерполяционная формула Ньютона для не равноотстоящих узлов
Пусть функция ¦(c), задана на сетке не равноотстоящих узлов xi , 
.Запишем следующие разделенные разности:
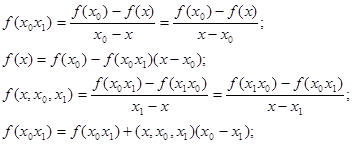
Выполним такие действия n-1 раз, получим: