Учебное пособие: Матрицы и определители

Умножение матрицы А на число λ приводит к умножению каждого элемента матрицы на число λ:

λА = 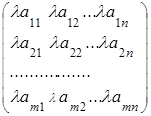, λR.

Из данного определения следует, что общий множитель всех элементов матрицы можно выносить за знак матрицы.

Пример.

Пусть матрица А =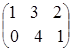, тогда 5А==.

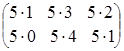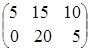Пусть матрица В = 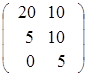= = 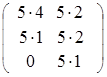5.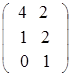

Свойства умножения матрицы на число :

1) λА = Аλ;

2) (λμ)А = λ(μА) = μ(λА), где λ,μ R;

3) (λА) = λА;

4) 0ּА = 0.

Сумма (разность) матриц .

Сумма (разность) определяется лишь для матриц одного порядка m´n.

Суммой (разностью) двух матриц А и В порядка m´n называется матрица С того же порядка, где = ± ( 1, 2, 3, …, m ,

j = 1, 2, 3, …, n.).

Иными словами, матрица С состоит из элементов, равных сумме (разности) соответствующих элементов матриц А и В.

Пример . Найти сумму и разность матриц А и В.

= , = ,

тогда =+==,

=–==.

Если же = , = , то А ± В не существует, так как матрицы разного порядка.

Из данных выше определений следуют свойства суммы матриц:

1) коммутативность А+В=В+А;

2) ассоциативность (А+В)+С=А+(В+С);

3) дистрибутивность к умножению на число λR: λ(А+В) = λА+λВ;

4) 0+А=А, где 0 – нулевая матрица;

5) А+(–А)=0, где (–А) – матрица, противоположная матрице А;

6) (А+В)= А+ В.

Произведение матриц.