Учебное пособие: Матрицы и определители

А=, В=

называется матрица С порядка m´k:

=∙, элементы которой вычисляются по формуле:

(1, 2, 3, …, m , j=1, 2, 3, …, k),

то есть элемент i –ой строки и j –го столбца матрицы С равен сумме произведений всех элементов i –ой строки матрицы А на соответствующие элементы j –го столбца матрицы В.

Пример . Найти произведение матриц А и В.

=, =,

∙===.

Произведение матриц В∙А не существует, так как матрицы В и А не согласованы: матрица В имеет порядок 2´2, а матрица А – порядок 3´2.

Рассмотрим свойства произведения матриц:

1 ) некоммутативность: АВ ≠ ВА, даже если А и В, и В и А согласованы. Если же АВ = ВА, то матрицы А и В называются коммутирующими (матрицы А и В в этом случае обязательно будут квадратными).

Пример 1 . = , = ;

==;

==.

Очевидно, что ≠ .

Пример 2 . = , = ;

= = =;

= = = .

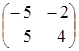Вывод: ≠, хотя матрицы и одного порядка.

2 ) для любых квадратных матриц единичная матрица Е является коммутирующей к любой матрице А того же порядка, причем в результате получим ту же матрицу А, то есть АЕ = ЕА = А.

Пример .

=, =;

===;

===.

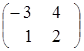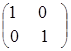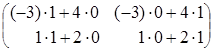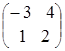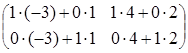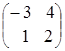3 ) A·0 = 0·A = 0.

4 ) произведение двух матриц может равняться нулю, при этом матрицы А и В могут быть ненулевыми.

Пример .

= , = ;

= ==.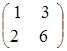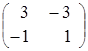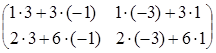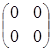