1. Понятие матрицы. Типы матриц

2. Алгебра матриц

Лекция 2. Определители

1. Определители квадратной матрицы и их свойства

2. Теоремы Лапласа и аннулирования

Лекция 3. Обратная матрица

1. Понятие обратной матрицы. Единственность обратной матрицы

2. Алгоритм построения обратной матрицы. Свойства обратной матрицы

4. Задачи и упражнения

4.1. Матрицы и действия над ними

4.2. Определители

4.3. Обратная матрица

5. Индивидуальные задания

Литература

ЛЕКЦИЯ 1. МАТРИЦЫ

План

1. Понятие матрицы. Типы матриц.

2. Алгебра матриц.

Ключевые понятия

Диагональная матрица.

Единичная матрица.

Нулевая матрица.

Симметричная матрица.

Согласованность матриц.

Транспонирование.

Треугольная матрица.

1. ПОНЯТИЕ МАТРИЦЫ. ТИПЫ МАТРИЦ

Прямоугольную таблицу

А=,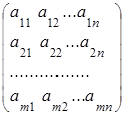

состоящую из m строк и n столбцов, элементами которой являются действительные числа , где i – номер строки, j - номер столбца на пересечении которых стоит этот элемент, будем называть числовой матрицей порядка m´n и обозначать .

Рассмотрим основные типы матриц:

1. Пусть m = n, тогда матрица А – квадратная матрица, которая имеет порядок n:

А = .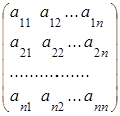

Элементы образуют главную диагональ, элементы образуют побочную диагональ.

Квадратная матрица называется диагональной , если все ее элементы, кроме, возможно, элементов главной диагонали, равны нулю:

--> ЧИТАТЬ ПОЛНОСТЬЮ <--