Учебное пособие: Матрицы и определители
5. Определитель равен нулю, если соответствующие элементы его строк (столбцов) пропорциональны:
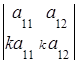 =0,
=0, 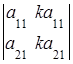 = 0.
= 0.
6. Если элементы одной строки (столбца) определителя равны сумме двух слагаемых, то такой определитель равен сумме двух определителей:
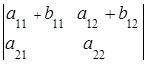 =
=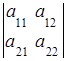 +
+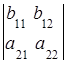 ,
, 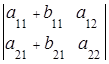 =
=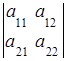 +
+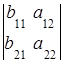 .
.
7. Значение определителя не изменится, если к элементам его строки (столбца) прибавить (вычесть) соответственные элементы другой строки (столбца), умноженные на одно и тоже число ![]() :
:
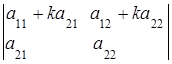 =
=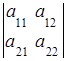 +
+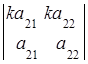 =
=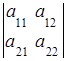 ,
,
так как 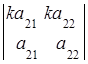 =0 по свойству 5.
=0 по свойству 5.
Остальные свойства определителей рассмотрим ниже.
Введем понятие определителя третьего порядка: определителем третьего порядка квадратной матрицы называется число
Δ =![]() = det A=
= det A= 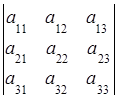 =
=
=![]()
![]()
![]() +
+![]()
![]()
![]() +
+![]()
![]()
![]() –
– ![]()
![]()
![]() –
– ![]()
![]()
![]() –
– ![]()
![]()
![]() ,
,
(2)
т. е. каждое слагаемое в формуле (2) представляет собой произведение элементов определителя, взятых по одному и только одному из каждой строки и каждого столбца. Чтобы запомнить, какие произведения в формуле (2) брать со знаком плюс, а какие со знаком минус, полезно знать правило треугольников (правило Саррюса):
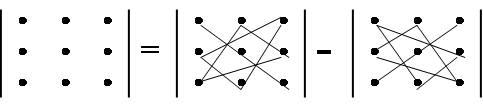 |
Пример . Вычислить определитель
![]() =
=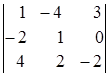 =
=
=![]() =
=
=![]() .
.
Следует отметить, что свойства определителя второго порядка, рассмотренные выше, без изменений переносятся на случай определителей любого порядка, в том числе и третьего.
2. ТЕОРЕМЫ ЛАПЛАСА И АННУЛИРОВАНИЯ
Рассмотрим еще два очень важных свойства определителей.
Введем понятия минора и алгебраического дополнения.
Минором элемента определителя называется определитель, полученный из исходного определителя вычеркиванием той строки и того столбца, которым принадлежит данный элемент. Обозначают минор элемента ![]() через
через ![]() .
.
Пример .![]() =
= 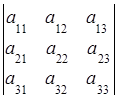 .
.
Тогда, например, ![]() =
= 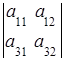 ,
, ![]() =
= 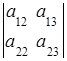 .
.
Алгебраическим дополнением элемента ![]() определителя
определителя ![]() называется его минор
называется его минор ![]() , взятый со знаком
, взятый со знаком ![]() . Алгебраическое дополнение будем обозначать
. Алгебраическое дополнение будем обозначать ![]() , то есть
, то есть ![]() =
=![]()
![]() .
.
Например:
![]() =
= 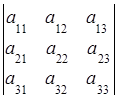 ,
, ![]() =
=![]()
![]() =
=![]()
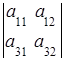 = –
= –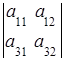 ,
,
![]() =
=![]()
![]() =
=![]()
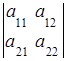 =
=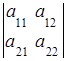 .
.
Вернемся к формуле (2). Группируя элементы и вынося за скобки общий множитель, получим:
![]() =
=![]() (
(![]()
![]() –
– ![]()
![]() ) +
) +![]() (
(![]()
![]() –
– ![]()
![]() ) +
) +![]() (
(![]()
![]() –
–![]()
![]() )=
)=