Учебное пособие: Матрицы и определители
![]() · (
· (![]() ·
·![]()
![]()
Пример .
Имеем матрицы 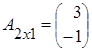 ,
, ![]() ,
, ![]()
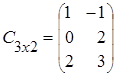 ;
;
тогда Аּ(ВּС) = ![]() (
(![]() ·
·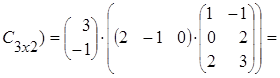
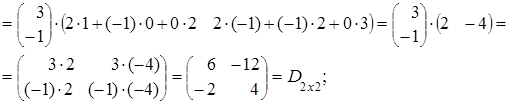
(АּВ)ּС=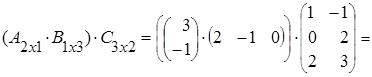
=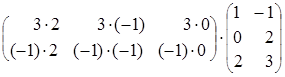 =
=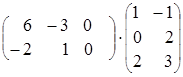 =
=
=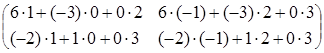 =
=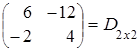 .
.
Таким образом, мы на примере показали, что Аּ(ВּС) = (АּВ)ּС.
6 ) дистрибутивность относительно сложения:
(А+В)∙С = АС + ВС, А∙(В + С)=АВ + АС.
7) (А∙В)![]() = В
= В![]() ∙А
∙А![]() .
.
Пример.
![]() =
=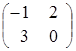 ,
, ![]() =
=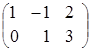 ,
,
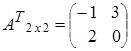 ,
, ![]() =
=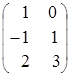 .
.
Тогда АВ =![]() ∙
∙![]() =
=![]()
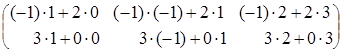 =
=
=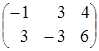
![]() (А∙В )
(А∙В )![]() =
= ![]() =
=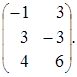
В ![]() ∙А
∙А ![]() =
=![]() ∙
∙![]() =
= 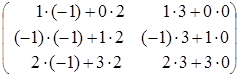 =
=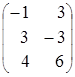 =
=![]() .
.
Таким образом, (А∙В )![]() = В
= В ![]() А
А ![]() .
.
8 ) λ(АּВ) = (λА)ּ В = Аּ (λВ), λ,![]() R.
R.
Рассмотрим типовые примеры на выполнение действий над матрицами, то есть требуется найти сумму, разность, произведение (если они существуют) двух матриц А и В.
Пример 1 .
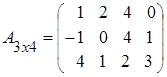 ,
, 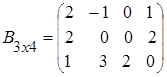 .
.
Решение.
1) ![]() +
+ ![]() =
= ![]() =
=  =
= ;
;
2)![]() –
– ![]() =
=![]() =
= =
= ;
;
3) произведение ![]()
![]() не существует, так как матрицы А и В несогласованы, впрочем, не существует и произведения
не существует, так как матрицы А и В несогласованы, впрочем, не существует и произведения ![]()
![]() по той же причине.
по той же причине.
Пример 2 .
![]() =
= ,
, ![]() =
=![]() .
.