Учебное пособие: Матрицы и определители

== АּВ=ВּА, т. е. данные матрицы коммутирующие.

ЛЕКЦИЯ 2. ОПРЕДЕЛИТЕЛИ

План

1. Определители квадратной матрицы и их свойства.

2. Теоремы Лапласа и аннулирования.

Ключевые понятия

Алгебраическое дополнение элемента определителя.

Минор элемента определителя.

Определитель второго порядка.

Определитель третьего порядка.

Определитель произвольного порядка.

Теорема Лапласа.

Теорема аннулирования.

1. ОПРЕДЕЛИТЕЛИ КВАДРАТНОЙ МАТРИЦЫ И ИХ СВОЙСТВА

Пусть А – квадратная матрица порядка n:

А=.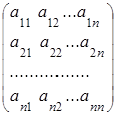

Каждой такой матрице можно поставить в соответствие единственное действительное число, называемое определителем (детерминантом) матрицы и обозначаемое

= det A= Δ=.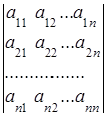

Отметим, что определитель существует только для квадратных матриц.

Рассмотрим правила вычисления определителей и их свойства для квадратных матриц второго и третьего порядка, которые будем называть для краткости определителями второго и третьего порядка соответственно.

Определителем второго порядка матрицы называется число, определяемое по правилу:

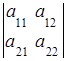== – , (1)

т. е. определитель второго порядка есть число, равное произведению элементов главной диагонали минус произведение элементов побочной диагонали.

Пример .

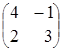=, тогда ==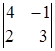 4 · 3 – ( –1) · 2=12 + 2 = 14.

Следует помнить, что для обозначения матриц используют круглые или квадратные скобки, а для определителя – вертикальные линии. Матрица – это таблица чисел, а определитель – число.

Из определения определителя второго порядка следуют его свойства :

1. Определитель не изменится при замене всех его строк соответствующими столбцами:

=.

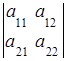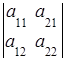2. Знак определителя меняется на противоположный при перестановке строк (столбцов) определителя:

= – , = – .

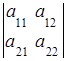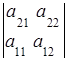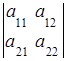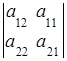3. Общий множитель всех элементов строки (столбца) определителя можно вынести за знак определителя:

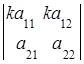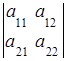= или 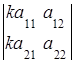=.
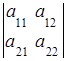