Лекция 1. Вводная

Начертательная геометрия — раздел геометрии, в котором пространственные формы с их геометрическими закономерностями изучаются в виде их изображений на плоскости.

Основоположником начертательной геометрии, как науки, является французский ученый 18 века Гаспар Монж, систематизировавший все существующие знания в этой области и создавший труд «Geometry descriptive», изданный в 1799 г.. Г. Монж говорил, что «…нужно приучить пользоваться начертательной геометрией всех способных молодых людей, как богатых, для того, чтобы они были в состоянии употреблять свои капиталы с пользой – равно для себя и государства, так и для тех, у которых образование является единственным богатством, для того, чтобы они могли увеличить цену своего труда».

В России впервые этот предмет был введен в Московском высшем училище в 1810 году в Институте путей сообщения в Петербурге.

«Чертеж – это язык техники», - говорил Г. Монж, а проф. Курдюмов продолжал эту мысль: «А начертательная геометрия - это грамматика этого языка, т.к. учит нас правильно читать чужие и излагать наши собственные мысли, пользуясь в качестве слов только линиями и точками, как элементами всякого изображения».

Начертательная геометрия ставит перед собой 2 задачи:

1. Прямая ― научиться изображать на плоскости по оригиналу трехмерные геометрические объекты.

2. Обратная ― по заданному чертежу восстановить положение оригинала в пространстве.

Существуют центральный и параллельный методы проецирования. Рассмотрим первый.

Метод центрального проецирования

Если дана некоторая плоскость П₁ , которую мы назовем плоскостью проекций, центр проекций S вне ее, а также точку А, то проведя через т. А из центра S проецирующий луч, мы получим проекцию т. А на пл. проекций П₁ . Если таких произвольно расположенных точек будет несколько, то в итоге мы получим некую коническую поверхность, поэтому этот метод называется еще и коническим. При таком способе проецирования нет размерного соответствия между изображением и моделью. (Рисунок 1)

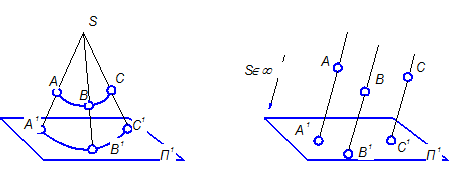
Рисунок 1 Рисунок 2

Метод параллельного проецирования

В тех случаях, когда размерное соответствие обязательно, используют метод параллельного или цилиндрического проецирования, когда центр проецирования находится в бесконечности и проецирующие лучи параллельны между собой (рисунок 2). В качестве фиксированного базиса используют три взаимно-перпендикулярных плоскости проекций.

Первая из них называется фронтальной плоскостью и обозначается латинской буквой V . Она стационарна. А проекциям точек этой плоскости присваивают индекс этой же плоскости, например А^v, А^н, А^w .

Вторая пл. проекций, расположенная горизонтально, так и называется – горизонтальная и обозначается - Н. Для получения плоского чертежа ее поворачивают относительно оси ох переднюю полу вниз, заднюю вверх.

Третья плоскость расположена, как и первая вертикально, но перпендикулярна к фронтальной, и разворачивается против часов стрелки вокруг оси oz при совмещении плоскостей в единую и называется профильной - W .

Эти три плоскости взаимно перпендикулярны и делят пространство на 8 углов – октантов.

Пересекаясь между собой, три плоскости образуют линии пересечения – оси.

V ∩ H Þox (ось абсцисс); H ∩ W Þoy (ось ординат); V ∩ W Þoz (ось аппликат).

Ниже на чертеже представлена модель пространства и рядом изображение ее на плоскости.

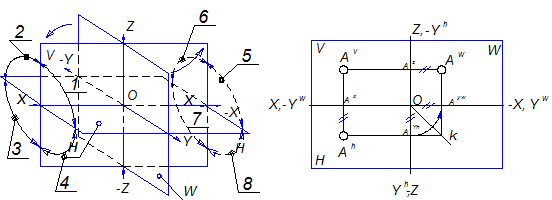
Рисунок 3 Рисунок 4

При этом следует помнить, что проецирующие лучи параллельны между собой и перпендикулярны к плоскостям проекций.

При проецировании мы будем использовать такие геометрические образы как точка, прямая, плоскость, объемные тела.

Точка

Точка – это геометрический образ, не имеющий измерений. Проекцией точки является основание перпендикуляра проецирующего луча, опущенного на плоскость проекций из заданной пространственной точки. Точка может быть задана на чертеже своими координатами, например: А (20;30;15;) или проекциями.

Х - указывает на расстояние до профильной плоскости проекций, Y – до фронтальной, Z – до горизонтальной.

Ортогональный чертеж точки образуется при проведении линий связи из соответствующих координат. На пересечении этих, перпендикулярных между собой линий и образуются проекции точек.

X,Y Þ A^h ; X,Z Þ A^v ; Y,Z Þ A^w .

Линия связи – это прямая, соединяющая две проекции точки. Следует помнить, что фронтальная A^v и профильная A^w проекции точки всегда находятся на горизонтальной линии связи, а фронтальная A^v и горизонтальная A^h -- на вертикальной

--> ЧИТАТЬ ПОЛНОСТЬЮ <--