Из точки А. опустить перпендикуляр на пл. Р.

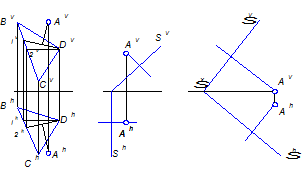
Рисунок 11

Задача 2

Из точки А плоскости Р восстановить перпендикуляр и, выбрав на нем произвольную точку, определить ее расстояние до этой плоскости.

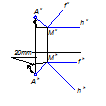
Рисунок 12

Плоскость, перпендикулярна к другой тогда, когда она проходит через прямую, перпендикулярную к этой плоскости (рисунки 13 а и в ).

Если следы плоскостей взаимно-перпендикулярны, это признак того, что плоскости не перпендикулярны.

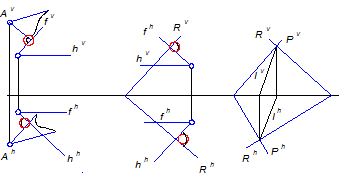
а) в) с)

Рисунок 13

Перпендикулярность геометрических элементов

Проецирование углов

1. Произвольный угол между двумя произвольными проецируется без искажения только на ту плоскость, которой он параллелен.

2. Теорема.

Прямой угол между двумя прямыми проецируется на плоскость в натуральную величину, если одна из сторон этого угла параллельна этой плоскости.

Рисунок 14

Проверьте себя:

1. Какие положения относительно друг друга занимают плоскости в пространстве?

2. В чем заключается признак параллельности двух плоскостей?

3. В чем заключается признак перпендикулярности двух плоскостей?

4. В чем заключается признак параллельности прямой и плоскости?

5. В чем заключается признак перпендикулярности прямой и плоскости?

6. В чем смысл теоремы прямого угла?

Лекция 6

Методы преобразования

Существует два метода преобразования:

Метод вращения, сущность которого заключается в том, что плоскости проекций остаются неизменными, а геометрический объект вращается в пространстве вокруг заданой оси таким образом, как это необходимо для решения задачи.

В свою очередь, метод вращения подразделяется на:

а) вращение вокруг осей перпендикулярных к плоскостям проекций:

На рисунке 1а – вокруг фронтально-проецирующей оси точка поворачивается на 30°, на 1б – вокруг горизонтально-проецирующей оси т. А вращается до совпадения с пл. Р