Учебное пособие: Надёжность функционирования автоматизированных систем

Функция представляет собой функцию распределения случайной величины Т.

События В и С несовместные события (в опыте не могут появиться вместе).

А = В + С; P(A) = P(B) + P(С);

откуда

P(С) = P(A) - P(B); P(A) = ; P(B) = ;

P(C) = ;

Следовательно

= - ;

или

= - ;

Введём в рассмотрение событие А. Событие А означает, что , т.е. в интервале времени от 0 до t отказа не произойдёт.

Введём в рассмотрение событие . Событие означает, что T < t , т.е в интервале времени от 0 до t произойдёт отказ. События A и являются противоположными, т.к. они образуют полную группу событий. События образуют полную группу, если в результате опыта одно из них обязательно должно произойти.

Из теории вероятностей известно, что сумма вероятностей противоположных событий равна единице, т.е.

P(A) + P;

P(A) = P(T ³ t) ; P= P(T<t) ;

Следовательно

P(T³t) + P(T < t) = 1 или

P(t) + q(t) = 1

Для вероятности безотказной работы справедливо приближённое соотношение

P(t) », где =

Здесь n(t) - число изделий, не отказавших к моменту времени t;

N - Число изделий, поставленных на испытания.

Испытания изделий должны проводиться при одинаковых условиях так, чтобы отказы изделий были независимы друг от друга.

Для вероятности отказа справедливо приближённое равенство

; где .

Здесь N - n(t) - число изделий, отказавших к моменту времени t.

1.8 Плотность вероятности f ( t ) времени безотказной работы T

; - частота отказов.

Здесь - плотность вероятности случайной величины T или частота отказов.

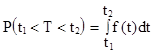® вероятность того, что отказ изделия произойдёт на интервале времени .