Дипломная работа: Диагностирование характеристик вала с дисками по собственным частотам его крутильных колебаний

Складывая эти уравнения получим

откуда

,

или

.

Квадрат частоты колебаний р² нулю равен быть не может, поэтому:

. (2.16)

Выразим М₁ и М₃ через М₂ , что может быть сделано из уравнения (2.15)

Подставим полученные значения М₁ и М₃ в уравнение (2.16)

Сокращая на М₂ и приводя к общему знаменателю получим:

или

Делаем группировку

Освобождаясь от коэффициента при р⁴ и делая преобразование в круглых скобках получим окончательно:

(2.17)

Получили биквадратное уравнение для определения частоты. Корни этого уравнения и соответствуют двум главным видам колебаний: низшему, имеющему один узел колебаний (два соседних диска вращаются в одну сторону), и высшему, имеющему два узла колебания (крайние диски вращаются в одну сторону).

1.4 Колебания вала с четырьмя дисками

Рассмотрим крутильные колебания вала с четырьмя дисками. Пусть I₁ , I₂ ,I₃ ,,I₄ — моменты инерции дисков, k₁ ,k₂ ,,k₃ — жесткости участков вала на основе формулы (1.1) равные:

; ;

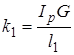Амплитуды колебаний дисков обозначим по-прежнему: М₁ ,М₂ ,,М₃ ,,М₄ .

Тогда уравнения (2.14) для данного случая примут вид:

(2.18)

Складывая полученные уравнения найдем:

Учитывая подобные слагаемые, получим