Дипломная работа: Диагностирование характеристик вала с дисками по собственным частотам его крутильных колебаний

Дифференцируя уравнение (2.6) найдем:

;

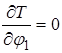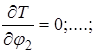
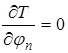
и дифференцируя уравнение (2.10)

; ;

;……;

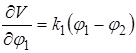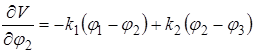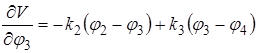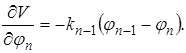
Дифференцируя уравнение (2.6) по получим:

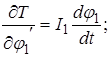
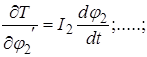
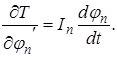
Полученные уравнения необходимо продифференцировать по времени

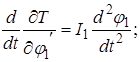
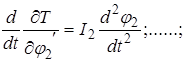
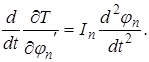
Располагая найденными выше величинами, можем составить систему дифференциальных уравнений движения рассматриваемой системы.

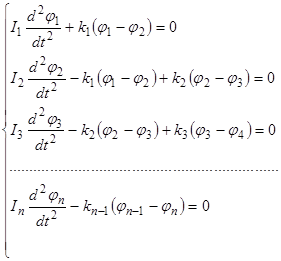(2.12)

Для решения полученной системы дифференциальных уравнений полагаем, что каждое колебательное движение системы (их будет столько же, сколько и степеней свободы, т. е. п) будет простым гармоническим. Частные решения системы (2.12), можно представить в виде:

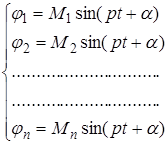. (2.13)

В этих уравнениях по-прежнему М амплитуда колебания, и р частота. Находим вторую производную от по времени:

.

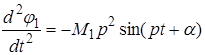Аналогично,

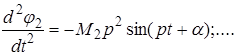
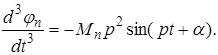
Подставляя значения и 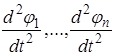в уравнения системы (2.12), получим систему обыкновенных уравнений со многими неизвестными для определения частоты колебания р.

Сокращая в данных уравнениях на получим окончательно

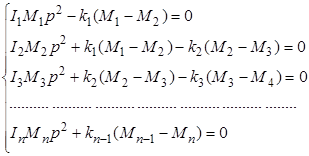(2.14)

Последовательно исключая неизвестные , получим уравнение для определения частоты р. Уравнение для определения частоты собственных колебаний, полученное в результате исключения из уравнений (2.14), называется характеристическим. Уравнения (2.14) могут быть применены для определения числа собственных крутильных колебаний системы с произвольным числом дисков. В тех случаях, когда получившееся характеристическое уравнение имеет высокую степень относительно р² (что бывает при системе со многими дисками), оно может быть решено графически либо каким-нибудь приближенным методом.

1.3 Колебания вала с тремя дисками

Рассмотрим колебания вала с тремя дисками (рис. 3). Здесь I₁ , I₂ ,I₃ моменты инерции дисков, k₁ и k₂ жесткости участков вала на кручении, по аналогии с формулой (1.1) равные:

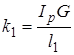и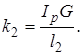

Рис. 3 Вал с тремя дисками

Если амплитуды колебаний дисков обозначить то уравнения (2.14) для данного случая примут вид: