Дипломная работа: Диагностирование характеристик вала с дисками по собственным частотам его крутильных колебаний

Уравнение движения тогда будет иметь вид:

Освобождаясь от коэффициента при дифференциале

и обозначая

(1.2)

получим

(1.3)

Решение этого уравнения может быть представлено в виде:

(1.4)

по аналогии получаем:

(1.5)

Очевидно, что мы в данном случае получили простое гармоническое колебание.

Круговая частота этого колебания (равная угловой скорости) будет

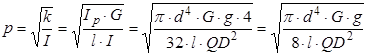(1.2а)

и период колебания

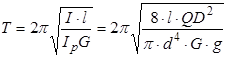(1.6)

Формулы (1.2а) и (1.6) справедливы в окончательном виде только для сплошного диска постоянной толщины, в случае какого-либо другого диска частоту и период следует определять по формулам:

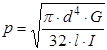(1.2)

и

. (1.)

Вычисляем в них соответствующий момент инерции диска по формулам теоретической механики.

Рассмотрим теперь случай колебаний вала с диском (рис. 1), с учетом массы вала. Помимо полярного момента инерции сечения вала, воспользуемся выражением для экваториального момента инерции (массы) вала, известным из теоретической механики.

где I₀ — экваториальный момент инерции,

W— собственный вес вала,

r—радиус вала.

Если вес единицы объема вала, т. е. его удельный вес, обозначить , то I₀ для круглого вала можно представить в виде:

(2.b)