Дипломная работа: Диагностирование характеристик вала с дисками по собственным частотам его крутильных колебаний

Из уравнений получим

и

и период колебания примет вид

(2.4)

частота колебаний будет:

(2.5)

Для изучения случаев колебания валов с большим числом дисков, чем два, удобнее в отличие от вышеприведенных случаев вала с одной и двумя массами найти уравнения движения вала с произвольным количеством масс и затем применять его для любого частного случая.

1.2 Решение прямой задачи для вала с n-дисками

Рассмотрим вал, несущий п- дисков. Пусть углы закручивания вала в местах насадки диска будут соответственно Жесткости I, II,..., n-1 участков вала, т. е. на основе обозначения (1.1) моменты, которые могут вызвать угол закручивания данного участка равный одному радиану, обозначим: k₁ , k_2,…, k_п-1. Моменты инерции дисков по-прежнему обозначим I₁ ,I₂ ,..,I_n . Для получения уравнения колебательного движения рассматриваемой нами системы применим уравнения Лагранжа, при пользовании которыми необходимо знать выражение для кинетической и потенциальной энергии системы. Кинетическая энергия диска, имеющего момент инерции I и угол закручивания , выражается формулой

Кинетическая энергия нашей системы слагается из суммы кинетической энергии всех дисков (кинетическую энергию вала мы тут не учитываем, считая момент инерции диска большим по сравнению с моментом инерции вала).

Кинетическая энергия всей системы

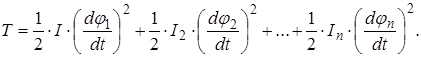(2.6)

Для нахождения потенциальной энергии системы, являющейся в данном случае энергией кручения, необходимо пользоваться формулой

,

где М - крутящий момент, действующий на данном участке, а - угол закручивания того же участка. Найдем крутящий момент и угол закручивания для первого участка нашей системы.

Если в месте насадки первого диска угол закручивания , а в месте насадки второго диска — ₂ , то угол закручивания на участке вала между дисками будет:

(2.7)

Для того чтобы вызвать угол закручивания первого участка вала величиной в I радиан, необходимо приложить крутящий момент величины k₁ , если же, как в нашем случае угол закручивания имеет ₁ -₂ радиан, то на валу действует крутящий момент величины

В нашем случае углы закручивания для участков вала будут:

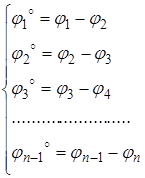(2.8)

и крутящие моменты:

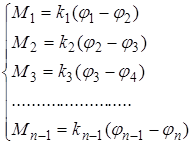(2.9)

Теперь можем составить выражение для потенциальной энергии системы, суммируя потенциальную энергию участков.

(2.10)

(так как 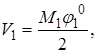то, подставляя значения ₁ из (2.8) и M₁ из (2.9) и аналогично для других участков получим формулу (2.10)).

В данном случае система имеет п степеней свободы, чему соответствует п обобщенных координат. Обобщенными координатами являются углы закручивания вала в местах насадки дисков. Уравнение Лагранжа, очевидно, придется составить по числу степеней свободы, т. е. также п. Для пользования уравнением Лагранжа в виде

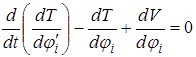(2.11)

необходимо найти частные производные от кинетической и потенциальной энергии системы, по обобщенным координатам и частные производные от кинетической энергии по дифференциалам обобщенных координат: