Дипломная работа: Дифференциальная геометрия поверхностей Каталана

Пусть .

Решим уравнение, например, для координаты .

Сделаем замену: .

.

.

Подставим в .

. Т.е. имеет вид:

Вычислим производные для проверки.

,

.

Теперь видно, что в каждой точке векторы и коллинеарные, поэтому смешанное произведение будет заведомо равно нулю (другого и быть не могло, собственно).

Теперь нам надо сделать так, чтобы нашлись 3 вектора не лежащие в одной плоскости (при соответствующих значениях параметра).

Т.е.

,

,

.

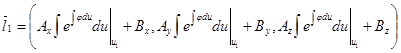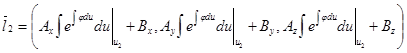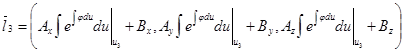И при этом: .

Поскольку сдвиг в пространстве всех этих трех векторов не повлияет на равенство (или не равенство) нулю смешанного произведения, то достаточно рассматривать векторы:

,

,

.

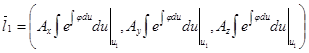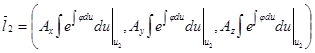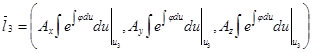А эти векторы, очевидно, лежат в одной плоскости. Так что добиться выполнения утверждения о коллинеарности векторов и в каждой точке, при выполнении, которого поверхность не будет являться поверхностью Каталана – нельзя.

Значит, стоит подумать о примере, который обеспечивает выполнение этого условия в одной точке, в которой, разумеется, мы должны «повернуть» плоскость образующих линейчатой поверхности.