Дипломная работа: Дослідження двовимірної квадратичної стаціонарної системи із двома приватними інтегралами у вигляді кривих другого порядку

g (1.37)

d (1.38)

Теорема 1.3 Система (1.1) має приватні інтеграли виду (1.3) і (1.13) з коефіцієнтами, певними формулами (1.32) - (1.38), за умови, що коефіцієнти системи (1.1) виражаються через параметри по формулах (1.28) - (1.31).

Нехай

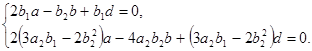(1.39)

З першого рівняння системи (1.39) знайдемо

, .

Підставляючи в друге рівняння системи (1.39), одержимо рівність:

(1.40)

Оскільки , те розглянемо два випадки: , тоді .

Зі співвідношень (1.25) при умовах (1.39) і (1.40) одержуємо, що коефіцієнти системи (1.1) визначаються наступними формулами:

, , (1.41)

, , , , (1.42)

Рівності (1.9) - (1.11), (1.19) - (1.22) за умови, що мають місце формули (1.41) - (1.42), дадуть наступні вираження для коефіцієнтів інтегралів (1.3) і (1.13):

a1 (1.43),a2 (1.44)

a3 (1.45), s (1.46)

(=0 (1.47)

g (1.48),

d (1.49)

Теорема 1.4 Система (1.1) має приватні інтеграли виду (1.3) і (1.13) з коефіцієнтами, певними формулами (1.43) - (1.49), за умови, що коефіцієнти системи (1.1) виражаються через параметри по формулах (1.41) - (1.42).

б) (1.50), (1.51)

З (1.50) знайдемо :

Зі співвідношень (1.25) при умовах (1.39) і (1.50) - (1.51) одержуємо, що коефіцієнти системи (1.1) визначаються наступними формулами:

, - будь-яке число, (1.52)

, , , , (1.53)

Рівності (1.9) - (1.11) і (1.19) - (1.22) за умови, що мають місце формули (1.52) - (1.53), дадуть наступні вираження для коефіцієнтів інтегралів (1.3) і (1.13):

(1=0 (1.54), a2 (1.55)

a (1.56)