Дипломная работа: Дослідження двовимірної квадратичної стаціонарної системи із двома приватними інтегралами у вигляді кривих другого порядку
,
Або
Характеристичними числами для крапки
системи (2.1) будуть
,
тобто
, 
.
Коріння 
- дійсні й різні знаки не залежно від параметра d. Виходить, крапка 
- сідло.
Досліджуємо нескінченно - вилучену частину площини наприкінці осі oy. Перетворення
[7]
переводить систему (2.1) у систему:
(2.6)
де 
.
Для дослідження станів рівноваги на кінцях осі y, нам необхідно досліджувати тільки крапку 
. Складемо характеристичне рівняння в крапці
.
Одержимо, що
Коріння - дійсні й одного знака. Отже, крапка 
- стійкий вузол.
Досліджуємо нескінченно - вилучену частину площини поза кінцями осі oy перетворенням [7] 
Це перетворення систему (2.1) переводить у систему:
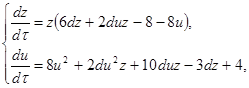(2.7)
де .
Вивчимо нескінченно - вилучені крапки на осі U, тобто при z=0. Маємо:
Одержуємо, що 
. Отже, станів рівноваги поза кінцями осі oy немає.
Тепер дамо розподіл станів рівноваги системи (2.1) у вигляді таблиці 1.
Таблиця 1.
|
К-во Просмотров: 428
Бесплатно скачать Дипломная работа: Дослідження двовимірної квадратичної стаціонарної системи із двома приватними інтегралами у вигляді кривих другого порядку
|