b (1.58)

g (1.59)

d (1.60)

Теорема 1.5 Система (1.1) має приватні інтеграли виду (1.3) і (1.13) з коефіцієнтами, певними формулами (1.54) - (1.60), за умови, що коефіцієнти системи (1.1) виражаються через параметри по формулах (1.52) - (1.53).

2. Якісне дослідження побудованих класів систем

2.1 Дослідження системи (1.1) з коефіцієнтами, заданими формулами (1.28) - (1.31)

Будемо проводити наше дослідження в припущенні, що , , .

Нехай ми маємо систему (1.1), коефіцієнти якої визначаються відповідно до формул (1.28) - (1.31), тоді система (1.1) запишеться у вигляді:

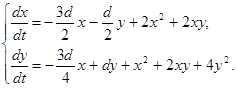(2.1)

Інтегральні криві в цьому випадку мають вигляд:

(2.2)

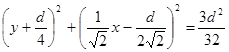(2.3)

Знайдемо стани рівноваги системи (2.1). Дорівнявши праві частини системи нулю й виключивши змінну y, одержимо наступне рівняння для визначення абсцис станів рівноваги:

(2.4)

З (2.4) одержуємо, що

, , , .

Ординати крапок спокою мають вигляд:

, , , .

Отже, маємо крапки

, , , .

Досліджуємо поводження траєкторій на околицях станів рівноваги , , , .

Досліджуємо крапку .

Складемо характеристичне рівняння в крапці .

Звідси

, (2.5)

,

Отже, характеристичне рівняння прийме вид:

= =0.

,

Або