Дипломная работа: Дослідження проблеми тригонометричних рівнянь

1. Якщо до нульового члена додати або відняти різниця прогресії , то від цього прогресія не зміниться, а тільки переміститься нульовий член, тобто зміниться нумерація членів.

2. Якщо коефіцієнт при змінній величині помножити на , то від цього відбудеться лише перестановка правої й лівої груп членів.

3. Якщо послідовних членів нескінченної прогресії

наприклад

, , , ...,

зробити центральними членами прогресій з однаковою різницею, рівної :

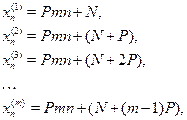
те прогресія й ряд прогресій виражають собою ті самі числа.

Приклад Ряд

може бути замінений наступними трьома рядами

, ,

4. Якщо нескінченних прогресій з однаковою різницею мають центральними членами числа, що утворять арифметичну прогресію з різницею , то ці рядів можуть бути замінені одною прогресією з різницею , і із центральним членом, рівним кожному із центральних членів даних прогресій, тобто якщо

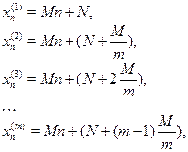
те ці прогресій поєднуються в одну

Приклад

, , ,

обидві поєднуються в одну групу

, тому що

Для перетворення груп, що мають загальні рішення, у групи, загальних рішень не дані групи, що мають, розкладають на групи із загальним періодом, а потім об'єднати групи, що вийшли, виключивши повторювані.

Розкладання на множники

Метод розкладання полягає в наступному: якщо

те всяке рішення рівняння

є рішення сукупності рівнянь