Дипломная работа: Дослідження проблеми тригонометричних рівнянь

те заміна приводить його до квадратного, оскільки

( ) і .

Якщо замість доданка буде, то потрібна заміна буде

Рівняння

зводиться до квадратного рівняння

поданням як . Легко перевірити, що при яких , не є коріннями рівняння, і, зробивши заміну , рівняння зводиться до квадратного.

Приклад Вирішити рівняння

Рішення. Перенесемо в ліву частину, замінимо її на

, і виразимо через і

Після спрощень одержимо

Розділимо по членне на , зробимо заміну :

Вертаючись до , знайдемо

Рівняння, однорідні відносно ,

Розглянемо рівняння виду

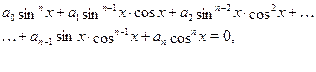
де , , , ..., , --- дійсні числа. У кожному складати^ся лівої частини рівняння ступеня одночленів рівні , тобто сума ступенів синуса й косинуса та сама й дорівнює . Таке рівняння називається однорідним відносно й , а число називається показником однорідності.

Ясно, що якщо , те рівняння прийме вид:

рішеннями якого є значення , при яких , тобто числа , . Друге рівняння, записане в дужках також є однорідним, але ступеня на 1 нижче.

Якщо ж , то ці числа не є коріннями рівняння .

При одержимо: , і ліва частина рівняння (1) приймає значення .

Отже, при , і , тому можна розділити обидві частини рівняння на . У результаті одержуємо рівняння: