Дипломная работа: Кинетические уравнения Власова

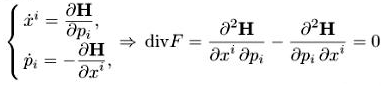
Получаем уравнения для функции распределения f(s,х,р) по координатам и импульсам (1.2) в виде

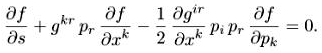(2.6)

Эго уравнение имеет вид

df/ds + {Н, f} = 0, где {Н, f} — скобка Пуассона:

Способ 2. Переход к инвариантной мере в пространстве координаты-скорости.

Пусть g — определитель матрицы gij. Вместо f в (2.5) введем новую функцию распределения

F{x,v,s) = F(x,v,s)/g.

Упражнение

Показать, что для новой функции распределения уравнение эволюции бездивергентно и имеет вид

Решение

Воспользуемся операцией дифференцирования определителя. При этом второе слагаемое в (2.5) преобразуется следующим образом:

В (a) используется тождество

Для новой функции распределения число частиц записывается в виде

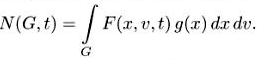
Поэтому g dxdv есть инвариантная мера: F не растет, т.е. полная производная от неё есть ноль, и поскольку число частиц сохраняется, то мера g dxdv сохраняется тоже.

Вывод. В качестве переменных в функции распределения можно брать импульсы или скорости, а в качестве времени — время или интервал s. Для простоты уравнений брали интервал, который в теории относительности называется собственным временем[7] . Возможность выбрать s в качестве параметра означает синхронизацию собственного времени различных частиц. С этим связан парадокс близнецов. Тот из них, чей интервал (собственное время) меньше, т.е. который «двигался больше», оказывается младше. Поэтому использование s хотя формально и возможно, но делает затруднительным интерпретацию результатов.

2.3 Как ведет себя мера риманова пространства при преобразованиях

Пусть проведена замена координат хк = f (). Как преобразуется при этом метрика? Имеем:

Поэтому где J — это det (дxi/д), Отсюда следует, что так как dx = |J|d, то = , т.е. —инвариант преобразований.

Дифференцируя по параметру, имеем , а поэтому dV=|J|dv. Отсюда следует, что g dxdv = - инвариантная мера, где каждый из сомножителей инвариантен при преобразованиях.

Вывод. В качестве переменных функции распределения удобно брать импульсы. В качестве параметра возьмем время, в качестве переменных функции распределения — t (время), х (пространственная координата), р(импульсы): f= f(t,x,p).

2.4 Вывод уравнения Власова-Максвелла

Система уравнений Власова-Максвелла описывает движение частиц в собственном электромагнитном поле. Стартуем с обычного действия для электромагнитного поля[8] , действия Власова-Максвелла или Лоренца (по повторяющимся верхним и нижним индексам идет суммирование):