Дипломная работа: Контрольные задания для заочников по математике

æ (2x2 + 3) /5приxÎ( - ¥, 1] ;

116. í 6 – 5xприxÎ (1, 3);

èx – 3приxÎ [3, +¥).

117. arctg.118. xctgx.

119. 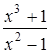.120.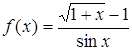

ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИЙ ОДНОЙ ПЕРЕМЕННОЙ И ЭЛЕМЕНТЫ ДИФФЕРЕНЦИАЛЬНОЙ ГЕОМЕТРИИ

121. -130. Найти производную функции одной переменной, исходя из определения производной.

y = tg2x.122. y = ln(3x + 1).123. y = cos(x2).

y = sin(x2 + 2x).125. y = ctg(3x - 2).126. y = Ö 2x2 + 1.

127. y = Ö 2 – cos3x.128. y = Ö 2 + sin2x.129. y = e2x.

y = (x + 1) /(x – 1).

131. -140. Найти производные первого порядка данных функций, используя правила вычисления производных.

1) y = Ö4x4 + tgx; 2) y = x1/2 / sinx;

3) y = ctg5x / x3; 4) y = arctg(ex) + tg(arccos(ex)).

1) y = ln(tg(3x + 2)); 2) y = Ö 1 – x2 arcsinx;

3) y = xtgx; 4) y = (x2 – 1) /(x2 + 1).

1) y = arccos(x2) + arcctg(x2); 2) xy = cos(x – y);

3) y = log2(2x + 1); 4) y = Ö1 – x2 / Ö1 + x2.

1) y = (2 - 5x) / Ö2 – 5x + x2; 2) y = ex – y;

3) y = 2 lnx – x; 4) y = sin2 3t, x = cos4 3t.

1) y = (arcsinx) 1 – x; 2) y = cos2 x + tg2x;

3) x3 + y3 – 3xy = 3; 4) x = t – sin2t, y = 1 – cos 2t.

1) y = sin2x/(1 + sin2x); 2) y = 3arctgx + (arctgx) 3,

3) y = (1 + x2) 1 + 2x; 4) y = tg3t, x = cos2 3t.

1) y = 3 –3x + (3x) –3; 2) y = (x – 1) log5(x2 – 1),

3) y = (x2 + 1) x; 4) y = tg(x2/y2).

1) y = ln(lg(log2x)); 2) y = (x2 + x + 1) /(x2 + 1);

3) y = (x + 1) x; 4) ex + y = x – y.

1) y = (x2 + 1) 3 – (x2 – 1) 3; 2) y = (ln5x) /(x4 – 1);

3) y = (tgx) ctgx; 4) x = t ctg(t2), y = t cos2(t2).