Дипломная работа: Линейные дифференциальные уравнения
(I) |A+B| ![]() |A|+|B|,
|A|+|B|,
(II) |AB| ![]() |A|*|B|,
|A|*|B|,
(III) |Ax| ![]() |A|*|x|,
|A|*|x|,
где А и В – матрицы, х – n-мерный вектор.
По определению, расстояние между двумя матрицами А и В равно |A-B|, и это расстояние удовлетворяет обычным свойствам метрики.
Нулевая матрица будет обозначаться через О, единичная – через Е. В случае опасности смешения размерностей эти квадратные матрицы порядка n будут обозначаться соответственно через Оn и Еn .
Заметим, что | Оn | = 0 и | Еn | = n, а не 1.
Комплексно сопряженной матрицей для А = (aij ) называется матрица ![]() , где
, где ![]() - комплексно сопряженные числа для aij . Транспонированная матрица обозначается через
- комплексно сопряженные числа для aij . Транспонированная матрица обозначается через ![]() и определяется так:
и определяется так: ![]() . Сопряженная матрица для А определяется так:
. Сопряженная матрица для А определяется так: ![]() . Заметим, что |A*|=|
. Заметим, что |A*|=|![]() |=|
|=|![]() |=|A|. Далее, (АВ)*=В*А*. Определитель матрицы А обозначается как det А.
|=|A|. Далее, (АВ)*=В*А*. Определитель матрицы А обозначается как det А.
Если det А = 0, то матрица А называется особой. Не особая матрица имеет обратную матрицу А-1 , которая удовлетворяет соотношениям
А А-1 = А-1А = Е.
Многочлен det (λЕ-А) степени n от λ называется характеристическим многочленом для матрицы А, а его корни – характеристическими корнями А. Если эти корни обозначены λi (i = 1, …, n), то
det (λЕ-А) = 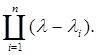
Две квадратные матрицы А и В порядка n называются подобными, если существует Неособая квадратная матрица Р порядка n, такая что
В = РАР-1.
Если А и В подобны, то они имеют один и тот же характеристический многочлен, ибо
det (λЕ-В) = det (Р(λЕ-А)Р-1 )= det Р* det (λЕ-А)* det Р-1 = det (λЕ-А).
В частности, коэффициенты многочлена det (λЕ-А) при степенях λ инвариантны относительно преобразования подобия. Два наиболее важных инварианта - det А и sp A – определитель и след А соответственно.
Приведем следующий фундаментальный результат о канонической форме матрицы.
Теорема 1.1 Каждая квадратная матрица А порядка n и подобная матрица вида
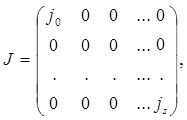
где J0 – диагональная матрица с элементами λ1 , λ2 ,…, λq и
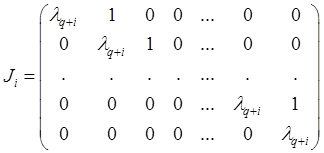 (i = 1, …, s).
(i = 1, …, s).
Здесь λj , j = 1, …, q+s, - характеристические корни А, не обязательно различные. Если λj – простой корень, то он встречается в J0 и поэтому, если все корни различны, А подобна диагональной матрице
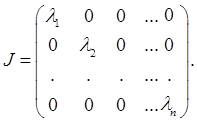
Из теоремы 1.1 непосредственно следует, что
det А = ![]() , spA =
, spA = ![]()
где произведение и сумма распространены на все корни, причем каждый корень считается столько раз, каков а его кратность. Матрицы Ji имеют вид
Ji = λq + i Еri +Zi ,
где Ji – квадратная матрица порядка ri и