Дипломная работа: Линейные дифференциальные уравнения

Если А = - А^* , то , будучи фундаментальной матрицей для системы (2.3), является также фундаментальной матрицей для системы (ЛО). Поэтому в силу теоремы 2.3 или

(2.6)

где С – постоянная неособая матрица. Из уравнения (2.6), в частности, следует, что эвклидова длина каждого вектора-решения системы (ЛО) постоянна.

Понижение порядка однородной системы. Если известно m (0<m<n) линейно зависимых решений системы (ЛО), то можно понизить порядок системы на m единиц, и следовательно, дело сведется к решению линейной системы порядка n-m.

Предположим, что φ₁ , φ₂ , …, φ_m - m линейно независимых векторов, которые являются решениями системы (ЛО) на интервале I. Пусть вектор φ_j имеет компоненты φ_ij (i = 1, …, n). Тогда ранг прямоугольной матрицы с элементами φ_ij (i = 1, …, n; j = 1, …, m) для каждого равен m, так как ее столбцы линейно независимы. Это означает, что для каждого в этой матрице найдется отличный от нуля определитель порядка m. Выберем некоторое и предположим для определенности, что в точке t₀ отличен от нуля определитель матрицы Ф_m с элементами φ_ij (i = 1, …, m; j = 1, …, m). Тогда в силу непрерывной зависимости определителя от его элементов φ_ij и непрерывности функций φ_ij в окрестности t₀ получим, что det Ф_m (t) 0 для t из некоторого интервала , содержащего t₀ . Пусть - один из таких интервалов; процесс понижения проведем для . (Идея этого процесса является модификацией метода вариации произвольных постоянных.)

Пусть матрица U имеет своими первыми m столбцами векторы φ₁ , φ₂ , …, φ_m и своими n-m столбцами – векторы е_m+1 , …, e_n , где e_j – вектор-столбец со всеми нулевыми элементами, кроме j-го, который равен 1. Очевидно, что U – неособая матрица на . Сделаем в (ЛО) подстановку

x = Uy. (2.7)

Заметим, что решениям х = φ_j (j = 1, …, m) при подстановке (2.7) соответствуют решения y = e_j (j = 1, …, m). Поэтому подстановку (2.7) можно рассматривать как систему относительно y, которая должна иметь решения e_j (j = 1, …, m).

Подставляя (2.7) в систему (ЛО), получаем

или в координатах,

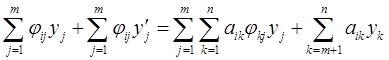(i = 1, …, m),

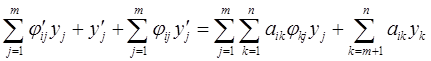(i = m+1, …, n).

Выражая то обстоятельство, что векторы φ_j с компонентами φ_{i j} являются решениями системы (ЛО), получаем

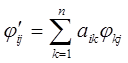(i = 1, …, n; j = 1, …, m),

откуда следует, что

(i = 1, …, m),

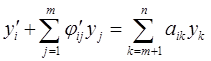(i = m+1, …, n). (2.8)

Так как det Ф_m 0, то из первых m уравнений (2.8) можно выразить производные (i = 1, …, m) через φ_{i j} , a_ik и y_k (k = m+1, …, n), и затем эти значения подставить в остальные формулы (2.8). Мы получим совокупность уравнений первого порядка, которым удовлетворяют функции y_i (i = m+1, …, n) вида

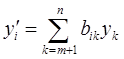(i = m+1, …, n), (2.9)

т.е. линейную систему порядка n-m.

Рассуждая в обратном порядке, предположим, что , …, ( имеет компоненты (i, j = m+1, …, n)) есть фундаментальная система решений на для системы (2.9). Пусть - матрица с элементами (i, j = m+1, …, n). Очевидно, что det 0 на . Для каждого j = m+1, …, n пусть (i = 1, …, m) определяется с помощью квадратур уравнений

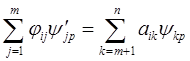(2.10)

(i = 1, …, m; p = m+1, …, n).

Пусть (p = m+1, …, n) обозначает с компонентами (i = 1, …, n) и пусть (p = 1, …, m). Так как (p = m+1, …, n) удовлетворяют системе (2.9) и первым m уравнениям (2.8), то они должны также удовлетворять остальным n-m уравнениям (2.8), и поэтому (p = m+1, …, n) являются решениями системы (2.8). таким образом, если Ψ – матрица со столбцами (p = m+1, …, n) и

Ф=U Ψ,

то Ф есть матрица-решение (ЛО) на I. U – неособая матрица.

Так как det =det на , то Ф есть неособая матрица на и, следовательно, является фундаментальным решением для системы (ЛО) на I.

Теорема 2.5. Пусть φ₁ , φ₂ , …, φ_m (m < n) – m известных линейно независимых решений системы (ЛО), причем φ_j (j = 1, …, m) имеют компоненты φ_{i j} (i = 1, …, n). Предположим, что определитель матрицы с элементами φ_{i j} (i, j = 1, …, m) на некотором подинтервале интервала i не обращается в нуль. Тогда с помощью подстановки (2.7) задачу определения n линейно независимых решений системы (ЛО) на можно свети к решению системы (2.9)порядка n-m и к квадратурам (2.10).