Дипломная работа: Линейные дифференциальные уравнения

Матрицы J_i можно представить также в виде λ_{q + i} Е_ri +γZ_i , где γ – любая постоянная, отличная от нуля.

Последовательность матриц {А_m } имеет своим пределом А, если для любого ε > 0 существует такое целое число N, что при p, q > N

|A_q - A_p | <ε.

Очевидно, что последовательность {А_m } сходится в том и только в том случае, когда сходится каждая из последовательностей компонент, а отсюда следует, что {А_m } сходится в том и только в том случае, когда существует предельная матрица, к которой и сходится эта последовательность.

Бесконечный ряд

называется сходящимся, если сходится последовательность частных сумм, а суммой ряда называется предельная матрица для частных сумм. Важное значение при изучении линейных уравнений имеет специальный ряд, который называется экспонентной матрицей А, а именно:

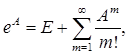(1.2)

где А_m есть m-я степень А. Ряд, определяющий е^А , сходится для всех А, июо для любых положительных целых p и q

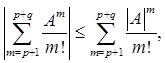
а последнее выражение есть разность Коши для ряда е^А , сходящегося для всех конечных |A|. Далее,

|е^А |(n-1) + е^|А| . (1.3)

Для матриц, вообще говоря, равенство е^А+В = е^А е^В неверно. Это равенство верно, если А и В коммутируют. Далее будет показано, что

det е^А = е^{sp А} , (1.4)

и поэтому е^А есть неособая матрица для всех А. Так как –А коммутирует с А, то е^-А = (е^А )^-1 .

Каждая матрица А удовлетворяет своему характеристическому уравнению det (λЕ-А) = 0, и это замечание часто бывает полезно для эффективного вычисления е^А .

Пусть В – неособая матрица. Покажем, что существует матрица А (называемая логарифмом В), такая, что е^А = В. В самом деле, если в имеет каноническую форму J теоремы 1, то А, очевидно, можно представить в виде

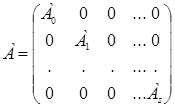
при условии, что е^{А i} = J_j , j = 0, 1, …, s. Легко также проверить, что А₀ можно представить в виде

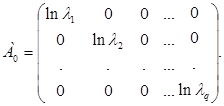
Далее,

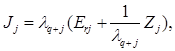
где Z_j – нильпотентная матрица, определенная в теореме 1.1. так как высшие степени Z_j равны нулю, то ряд

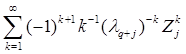
содержит лишь конечное число членов и поэтому сходится. Положим, по определению, сумму этого ряда, который на самом деле является многочленом от, равной

Таким образом,

есть многочлен от . С другой стороны. Из тождества