Дипломная работа: Некоторые линейные операторы

Содержание

Введение

§1. Определение линейного оператора. Примеры

§2. Непрерывные линейные операторы в нормированном пространстве. Ограниченность и норма линейного оператора

§3. Обратный оператор. Спектр оператора и резольвента

§4. Оператор умножения на непрерывную функцию

§5. Оператор интегрирования

§6. Оператор дифференцирования

§7. Оператор сдвига

Заключение

Введение

Наиболее доступными для изучения среде операторов, действующих в линейных нормированных пространствах, являются линейные операторы. Они представляют собой достаточно важный класс операторов, так как среди них можно найти операторы алгебры и анализа.

Целью дипломной работы является показать некоторые из линейных операторов, исследовать их на непрерывность и ограниченность, найти норму ограниченного оператора, а также спектр оператора и его резольвенту.

В первом и втором параграфах приведены основные сведения теории операторов: определение линейного оператора, непрерывности и ограниченности линейного оператора, его нормы. Рассмотрены некоторые примеры.

В третьем параграфе даны определения обратного оператора, спектра оператора и его резольвенты. Рассмотрены примеры.

В четвертом параграфе исследуется оператор умножения на непрерывную функцию: Ах(t) = g(t)x(t).

В пятом параграфе приведен пример оператора интегрирования Аf(t)=.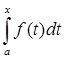

В седьмом параграфе исследуется оператор сдвига Af(x) = f(x+a).

Показана линейность, непрерывность, ограниченность, найдена норма, точки спектра и резольвента всех трех операторов.

В шестом параграфе исследуется оператор дифференцирования Дf(x)=f^/ (x), в пространстве дифференцируемых функции D_{[ a , b ]} . Показана его линейность. Доказано, что Д не является непрерывным оператором, а также как из неограниченности оператора следует его разрывность.

§1. Определение линейного оператора. Примеры

Определение 1. Пусть E_x и E_y [1] – линейные пространства над полем комплексных (или действительных) чисел. Отображение А: E_x ® E_y называется линейным оператором , если для любых элементов х₁ и х₂ пространства E_x и любого комплексного (действительного) числа выполняются следующие равенства [2] :

1. А(х₁ +х₂ ) = Ах₁ + Ах₂ ;

2. А(х) = А(х);

Примеры линейных операторов:

1) Пусть Е = Е₁ – линейное топологическое пространство. Оператор А задан формулой:

Ax = x для всех x Е.

Такой оператор, переводящий каждый элемент пространства в себя является линейным и называется единичным оператором.

2) Рассмотрим D_{[ a , b ]} – пространство дифференцируемых функций, оператор дифференцирования Д в пространстве D_{[ a , b ]} задан формулой:

Дf(x) = f^/ (x).

Где f(x) D_{[a, b]} , f^/ (x) C_{[a, b]} .

Оператор Д определен не на всем пространстве C_{[ a , b ]} , а лишь на множестве функций имеющих непрерывную производную. Его линейность, очевидно, следует из свойств производной.

3) Рассмотрим пространство С_{[-, +]} – пространство непрерывных и ограниченных функций, оператор А сдвигает функцию на const a:

Аf(x) = f(x+a).

Проверим линейность оператора А:

1) А(f+g) = (f+g)(x+a) = f(x+a) + g(x+a) = А(f) + А(g).

Исходя из определения суммы функции, аксиома аддитивности выполняется.

2) A(kf(x)) = kf(x+a) = kA(f(x)).

Верна аксиома однородности.

Можно сделать вывод, что А – линейный оператор.

4) Пусть (пространство непрерывных функций на отрезке [0,1], и дано отображение ₁ , заданное формулой:

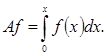
--> ЧИТАТЬ ПОЛНОСТЬЮ <--