Дипломная работа: Некоторые линейные операторы
Введем следующую терминологию. Число λ мы назовем регулярным для оператора А, действующего в линейном нормированном пространстве Е, если оператор (А – λI)-1 , называемый резольвентой оператора А, определен на всем пространстве Е и непрерывен. Совокупность всех остальных значений λ называется спектром оператора А. Спектру принадлежат все собственные значения оператора А, так как, если (А – λI)х=0 при некотором х≠0, то оператор (А – λI)-1 не существует. Их совокупность называется точечным спектром . Остальная часть спектра, то есть совокупность тех λ, для которых (А – λI)-1 существует, но не непрерывен, называется непрерывным спектром. Итак, каждое значение λ является для оператора А или регулярным, или собственным значением, или точкой непрерывного спектра. Возможность наличия у оператора непрерывного спектра – существенное отличие теории операторов в бесконечномерном пространстве от конечномерного случая.
Определение 8. Оператор 
, где 
– регулярная точка оператора А, называется резольвентой[6] оператора А и обозначается 
(или 
).
Теорема 5. Пусть 
– линейный непрерывный оператор, 
его регулярные числа. Тогда 
.
Доказательство. Умножим обе части равенства на 
: (
=
=
. С другой стороны получим 
. Так как числа 
– регулярные для оператора А, то оператор имеет обратный. Значит, из равенства 
следует, что 
. Значит, утверждение теоремы верно.
т. д-на.
Примеры.
1) Рассмотрим в пространстве C[0,1] оператор умножения на независимую переменную t: Ax = tx(t).
Уравнение Аx=
x принимает в этом случае вид:
tx(t) - x(t) = y(t),
решение x(t) этого уравнения есть функция, тождественно ему удовлетворяющая.
Если лежит вне отрезка [0, 1], то уравнение Аx=
x имеет при любом y(t) единственное непрерывное решение:
x(t) = 
y(t),
откуда следует, что все такие значения параметра являются регулярными, и резольвента есть оператор умножения на :
R
(y) = y(t).
Все значения параметра, принадлежащие отрезку[0, 1], являются точками спектра. В самом деле, пусть 0 
[0, 1]. Возьмем в качестве y(t) какую-нибудь функцию, не обращающуюся в нуль в точке 0 , y(0 ) = a 
0. Для такой функции равенство (t - 0 )x(t) = y(t), не может тождественно удовлетворяться ни при какой непрерывной на отрезке [0, 1] функции x(t), ибо в точке t = 0 левая часть его равна нулю, в то время как правая отлична от нуля. Следовательно, при = 0 уравнение Аx=x не имеет решения для произвольной правой части, что и доказывает принадлежность 0 спектру оператора A. Вместе с тем ни одна точка спектра не является собственным значением, так как решение однородного уравнения (t - )x(t) = 0, [0, 1], при любом t, отличном от , а следовательно, в силу непрерывности и при t = , обращается в нуль, т.е. тождественно равно нулю.
2) Пусть оператор А действующий из Е 
Е, задается матрицей А=
.
Аx = 
= 
.
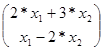Введем обозначения:
= y1
= y2
x1 , x2 , y1 , y2 E;
A - *I = 
, найдем определитель A - *I:
D(A - *I) = 
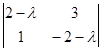= (2-)*(-2-) – 3 = 2 – 7;
Если определитель отличен от нуля, то есть если не есть корень уравнения 2 – 7 = 0, следовательно, все такие значения параметра регулярные.
Корни уравнения 2 – 7 = 0 образуют спектр:
1 = 
; 2 = -;
1 , 2 – собственные значения.
Найдем собственные векторы для собственных значений :
при = получаем:
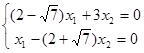
откуда x1 = (2+)x2 ; 1-й собственный вектор: ((2+)x, x);
при = - получаем:
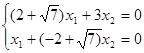
откуда x1 = (2 - )x2 ; 2-й собственный вектор: ((2 - )x, x);