Дипломная работа: Некоторые вопросы геометрии Лобачевского на модели Пуанкаре

Таким образом, точки окружности (O,r) и только они, являются при неподвижными.

Легко выполнить построение точки, инверсной данной. Рассмотрим три возможных случая:

1) |OA|=r, то A'=A.

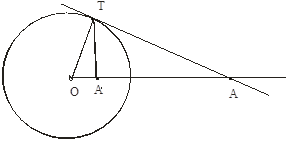
2) |OA|>r. Проведём [OA). Через точку А проводим касательную к (O, r). Пусть Т - точка касания. Проведём из Т перпендикуляр на [OA). Основание этого перпендикуляра и есть искомая точка А'. Действительно, из прямоугольного ОТА имеем |OA|·|OA'|==.

3) |OA|<r. В силу свойства получаем

следующее построение: восставляем в точке А перпендикуляр к [OA), в точке пересечения этого перпендикуляра с (O, r) проводим касательную к (O, r) и в пересечении касательной с [OA) получаем искомую точку А'.

Продолжим рассмотрение свойств инверсии.

. Пусть AПи ВПи (A) =A', (B) =B'.

Тогда

Доказательство.

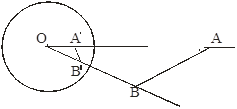
ОАВ~ОВ'А',

тогда

.

Учитывая, что

,

получаем

Введём понятие сложного отношения четырёх точек.

Определение.

.

. Инверсия сохраняет сложное отношение четырёх точек.

Доказательство. Даны точки A, B, C, D. (A) =A',

(B) =B', (C) =C', (D) =D'. Используя предыдущее свойство, имеем:

.