Дипломная работа: Некоторые вопросы геометрии Лобачевского на модели Пуанкаре

Аналогично доказывается следующая.

Теорема 2 . Если прямая проходит через центр инверсии, то она преобразуется при инверсии в себя; если прямая не проходит через центр инверсии, то она преобразуется в окружность, проходящую через центр инверсии.

4. Сохранение углов при инверсии

Определение. Прямые a и b назовём антипараллельными относительно О, если.

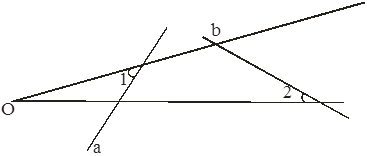
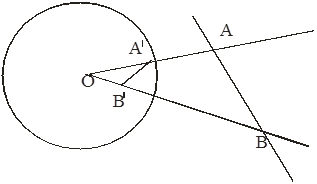
Лемма. Если (A) =A' и (B) =B', то прямые АВ и А'В' антипараллельны.

Доказательство получим, рассмотрев ОАВ и ОА'В'.

Теорема 3. Инверсия сохраняет величину углов.

Доказательство. Пусть f и g -кривые, выходящие из точки А, f '= (f ), g '= (g ) и A'= (A).

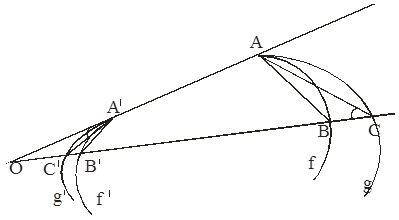
Проводим из точки О луч, пересекающий f и g в точках В и С соответственно. Пусть B'= (B), C'= (C). По лемме прямые АВ и А'В', АС и А'С' антипараллельны. Значит, OA'B'=OBA

и OA'C'=OCA, тогда

C'A'B'=OA'B' - OA'C'=OBA-OCA=CAB.

Переходя в равенстве C'A'B'=CAB к пределу при АОС0 (луч ОС приближаем к лучу ОА), получим утверждение теоремы.

Замечание. Доказанное свойство позволяет легко строить образы прямых и окружностей при инверсии.

Пусть, например, дана прямая L и

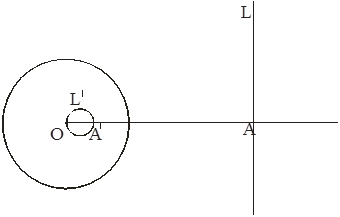
Проведём луч l с началом О, перпендикулярно L.

Пусть A'= (A).

В силу теорем 2 и 3 заключаем, что L'= (L) - окружность с диаметром ОА'.

5. Инвариантные прямые и окружности

Из теоремы 2 следует, что прямые, проходящие через центр инверсии, и только они, отображаются при на себя, т.е. эти прямые инвариантны при .

Мы уже отмечали, что ( (O,r)) = (O,r), т.е. окружность (O,r) инвариантна при .

Существуют ли другие окружности, инвариантные при ? Ответ на этот вопрос даёт следующая.

Теорема 4. Пусть S-окружность, отличная от (O,r). (S) =S тогда и только тогда, когда S ортогональна (O,r),

Доказательство. Допустим, что (S) =S. Ясно, что S пересекает (O,r) в двух точках, скажем, A и B.

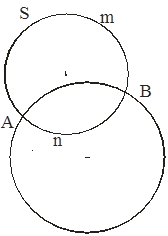
Имеем .

Согласно теореме 3

( (O,r) ^) = ( (O,r) ^),